题目内容
已知函数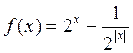
(1)若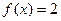 ,求
,求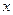 的值;
的值;
(2)若对任意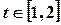 ,
,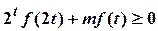 恒成立,求实数
恒成立,求实数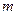 的取值范围。
的取值范围。
(1)当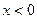 时,
时,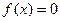
当 时,
时,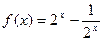 ,由条件可知
,由条件可知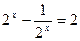 ,即
,即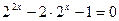 ,
,
解得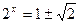 ,
,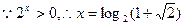
(2)当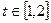 时,
时,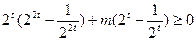 ,
,
即,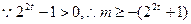
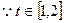 ,
,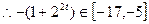 补缺 故
补缺 故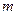 的取值范围是
的取值范围是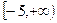
解析

练习册系列答案
相关题目
题目内容
已知函数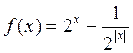
(1)若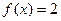 ,求
,求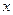 的值;
的值;
(2)若对任意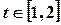 ,
,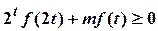 恒成立,求实数
恒成立,求实数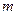 的取值范围。
的取值范围。
(1)当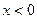 时,
时,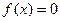
当 时,
时,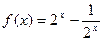 ,由条件可知
,由条件可知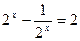 ,即
,即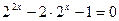 ,
,
解得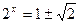 ,
,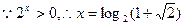
(2)当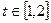 时,
时,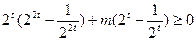 ,
,
即,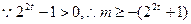
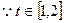 ,
,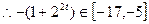 补缺 故
补缺 故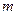 的取值范围是
的取值范围是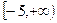
解析
