题目内容
已知函数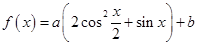 .
.
(1)当A=1时,求f(x)的单调递增区间;
(2)当A>0,且x∈[0,π]时,f(x)的值域是[3,4],求A,b的值.
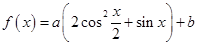 .
.(1)当A=1时,求f(x)的单调递增区间;
(2)当A>0,且x∈[0,π]时,f(x)的值域是[3,4],求A,b的值.
(1)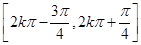 (k∈Z);(2)
(k∈Z);(2)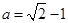 ,
,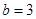 .
.
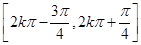 (k∈Z);(2)
(k∈Z);(2)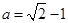 ,
,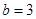 .
.试题分析:(1)将
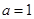 代入,利用倍角公式,辅助角公可得
代入,利用倍角公式,辅助角公可得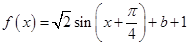 ,利用
,利用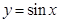 的单调递增区间,将
的单调递增区间,将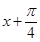 看成整体可得
看成整体可得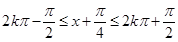 ,整理可得递增区间;(2)原函数化简可得
,整理可得递增区间;(2)原函数化简可得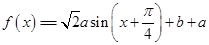 ,x∈[0,π]时,
,x∈[0,π]时,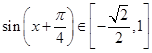 ,可得值域与[3,4]比较,可得关于
,可得值域与[3,4]比较,可得关于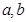 的方程组,解得
的方程组,解得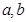 的值.
的值.解:(1)因为
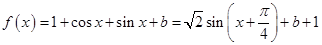 , 2分
, 2分由
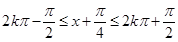 (k∈Z),得
(k∈Z),得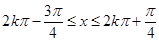 (k∈Z),
(k∈Z),所以f(x)的单调递增区间为
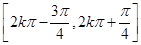 (k∈Z). 6分
(k∈Z). 6分(2)因为
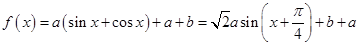 , 7分
, 7分因为x∈[0,π],则
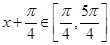 ,
,所以
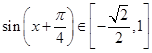 . 8分
. 8分故
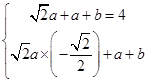 , 10分
, 10分所以
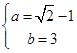 . 12分
. 12分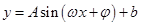 的性质.
的性质.
练习册系列答案
相关题目
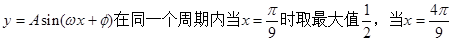 时取最小值
时取最小值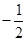 ,则该函数的解析式为( )
,则该函数的解析式为( )



 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是 ,且满足,
,且满足,
 的单调递减区间;
的单调递减区间; ,求△ABC的面积。
,求△ABC的面积。 的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若
的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若 ,则
,则 的值为( )
的值为( )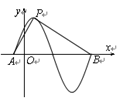


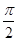

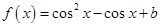 ,
,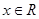 .
.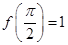 ,求函数
,求函数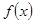 的解析式;
的解析式;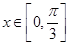 时,
时,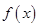 的图像与
的图像与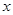 轴有交点,求实数
轴有交点,求实数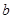 的取值范围.
的取值范围.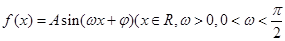 的部分图像如图所示.则函数f(x)的解析式为( )
的部分图像如图所示.则函数f(x)的解析式为( )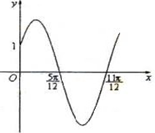
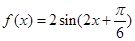
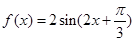
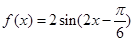
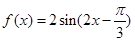
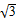 sinωxcosωx-cos2ωx,其中ω为使f(x)能在x=
sinωxcosωx-cos2ωx,其中ω为使f(x)能在x=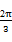 时取得最大值的最小正整数.
时取得最大值的最小正整数. )+
)+ 是奇函数,且在[0,
是奇函数,且在[0, ]上是减函数的
]上是减函数的 sin3x+cos3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是 .
sin3x+cos3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是 .