题目内容
已知函数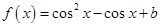 ,
,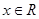 .
.
(1)若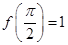 ,求函数
,求函数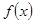 的解析式;
的解析式;
(2)若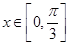 时,
时,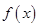 的图像与
的图像与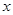 轴有交点,求实数
轴有交点,求实数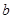 的取值范围.
的取值范围.
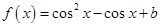 ,
,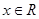 .
.(1)若
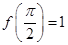 ,求函数
,求函数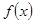 的解析式;
的解析式;(2)若
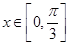 时,
时,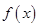 的图像与
的图像与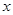 轴有交点,求实数
轴有交点,求实数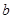 的取值范围.
的取值范围.(1)  ;(2)
;(2) 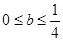 .
.
 ;(2)
;(2) 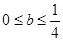 .
.试题分析:(1)
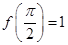 ,代入可求得
,代入可求得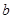 ;
;(2)
 ,
,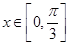 ,所以
,所以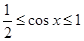 ,
,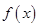 的图像与
的图像与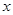 轴有交点,根据图形可得:
轴有交点,根据图形可得: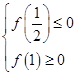 ,可以得到
,可以得到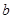 的取值范围.
的取值范围.(1)
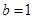 (2分)
(2分)(2)
 .(4分)
.(4分)又
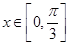 ,所以
,所以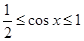
要使
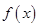 的图像与
的图像与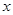 轴有交点,则
轴有交点,则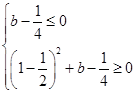 (8分)
(8分)解得
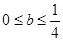 (10分)
(10分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图象沿
的图象沿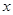 轴向左平移
轴向左平移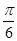 个单位后,得到一个关于
个单位后,得到一个关于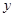 轴对称的图象,则
轴对称的图象,则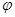
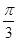
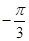
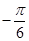
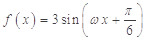 ,
,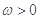 ,
,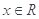 ,且以
,且以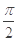 为最小正周期.
为最小正周期.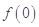 ;
;
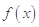 的解析式;
的解析式;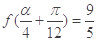 ,求
,求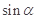 的值.
的值.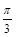 )的图象,只需把余弦曲线y=cosx上的所有的点 ( )
)的图象,只需把余弦曲线y=cosx上的所有的点 ( )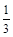 个单位长度
个单位长度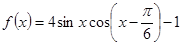 ,求函数
,求函数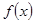 的最小正周期;
的最小正周期;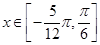 时,求函数
时,求函数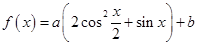 .
.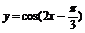 的单调减区间是 .
的单调减区间是 .  满足下了列哪些条件(填序号)__________.
满足下了列哪些条件(填序号)__________.
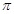 为最小周期;
为最小周期; 上单调递增;
上单调递增; 成中心对称.
成中心对称.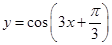 的图象可以先由y=cosx的图象向 平移 个单位,然后把所得的图象上所有点的横坐标 为原来的 倍(纵坐标不变)而得到。
的图象可以先由y=cosx的图象向 平移 个单位,然后把所得的图象上所有点的横坐标 为原来的 倍(纵坐标不变)而得到。