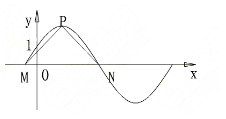
题目内容
已知向量
=(-3,0),
=(2,0)
(1)若向量
=(0,1),求向量
-
与
-
的夹角;
(2)若向量
满足|
|=1,求向量
-
与
-
的夹角最小值的余弦值.
| a |
| b |
(1)若向量
| c |
| a |
| c |
| b |
| c |
(2)若向量
| c |
| c |
| a |
| c |
| b |
| c |
(1)由题意可得向量
-
=(-3,-1),
-
=(2,-1),
设向量
-
与
-
的夹角为θ,则由cosθ=
=
=-
,
∴向量
-
与
-
的夹角为
.
(2)∵向量
满足|
|=1,
∴向量
的轨迹是半径为1的圆,
则向量
-
=
,
-
=
,则由图象可知当A位于y轴(0,1),
此时向量
-
与
-
的夹角最小,此时
=(0,1),
则
-
=(-3,-1),
-
=(2,-1),
则cosθ=
=
=-
,
即向量
-
与
| a |
| c |
| b |
| c |
设向量
| a |
| c |
| b |
| c |
(
| ||||||||
|
|
| -6+1 | ||||
|
| ||
| 2 |
∴向量
| a |
| c |
| b |
| c |
| 3π |
| 4 |
(2)∵向量
| c |
| c |
∴向量
| c |
则向量
| a |
| c |
| AC |
| b |
| c |
| AB |
此时向量
| a |
| c |
| b |
| c |
| c |
则
| a |
| c |
| b |
| c |
则cosθ=
(
| ||||||||
|
|
| -6+1 | ||||
|
| ||
| 2 |
即向量
| a |
| c |


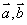 ,下列命题中错误的是( )
,下列命题中错误的是( )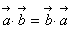
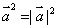
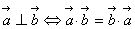

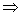
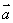 在
在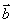 上的投影为
上的投影为