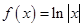题目内容
等比数列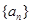 中,
中,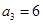 ,前三项和
,前三项和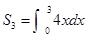 ,则公比
,则公比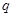 的值为
的值为
A.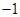 或 或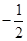 | B.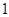 或 或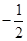 | C.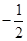 | D.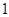 |
B
解析试题分析:解:∵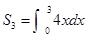 =18,,∴a1+a2=
=18,,∴a1+a2= (1+q)=12,⇒2q2-q-1=0,⇒q=1或q=
(1+q)=12,⇒2q2-q-1=0,⇒q=1或q=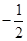 ,故选B
,故选B
考点:等比数列的前n项和, 定积分的基本运算
点评:本题考查等比数列的前n项和、定积分的基本运算,求定积分关键是找出被积函数的原函数,本题属于基础题.

练习册系列答案
相关题目
已知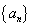 是首项为1的等比数列,
是首项为1的等比数列, 是
是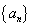 的前n项和,且
的前n项和,且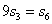 ,则数列
,则数列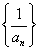 的前5项和为
的前5项和为
A.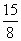 或5 或5 | B.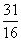 或5 或5 | C.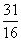 | D.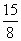 |
设等比数列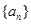 的公比
的公比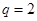 ,前n项和为
,前n项和为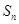 ,则
,则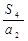 的值是( )
的值是( )
A.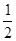 | B.4 | C.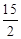 | D.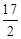 |
等比数列 中,
中,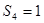 ,
,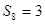 ,则
,则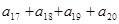 的值是( )
的值是( )
| A.14 | B.18 | C.16 | D.20 |
一个等比数列 的前n项和为48,前2n项和为60,则前3n项和为( )
的前n项和为48,前2n项和为60,则前3n项和为( )
| A.63 | B.108 | C.75 | D.83 |
设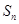 是等比数列
是等比数列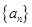 的前n项和,
的前n项和,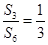 ,则
,则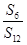 等于( )
等于( )
A.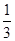 | B. | C.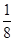 | D.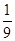 |
已知数列 是等差数列,
是等差数列,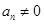 若
若 ,则
,则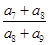 的值是( )
的值是( )
A.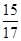 | B.1或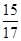 | C.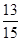 | D.1或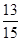 |
 满足:
满足: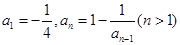 ,则
,则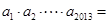 .
. 上的函数
上的函数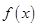 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
,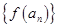 仍是等比数列,则称
仍是等比数列,则称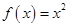 ②
②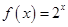 ③
③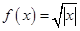 ④
④