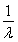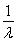题目内容
设数列{bn}满足bn＋2＝－bn＋1－bn(n∈N*)，b2＝2b1.
(1)若b3＝3，求b1的值；
(2)求证数列{bnbn＋1bn＋2＋n}是等差数列；
(3)设数列{Tn}满足：Tn＋1＝Tnbn＋1(n∈N*)，且T1＝b1＝－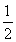
，若存在实数p，q，对任意n∈N*都有p≤T1＋T2＋T3＋…＋Tn＜q成立，试求q－p的最小值．
（1）b1＝－1（2）见解析（3）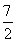
【解析】(1)∵bn＋2＝－bn＋1－bn，
∴b3＝－b2－b1＝－3b1＝3，
∴b1＝－1；(3分)
(2)∵bn＋2＝－bn＋1－bn①，
∴bn＋3＝－bn＋2－bn＋1②，
②－①得bn＋3＝bn，(5分)
∴(bn＋1bn＋2bn＋3＋n＋1)－(bnbn＋1bn＋2＋n)＝bn＋1bn＋2(bn＋3－bn)＋1＝1为常数，
∴数列{bnbn＋1bn＋2＋n}是等差数列．(7分)
(3)∵Tn＋1＝Tn·bn＋1＝Tn－1bnbn＋1＝Tn－2bn－1bnbn＋1＝…＝b1b2b3…bn＋1
当n≥2时Tn＝b1b2b2…bn(*)，
当n＝1时，T1＝b1适合(*)式
∴Tn＝b1b2b3…bn(n∈N*)．(9分)
∵b1＝－
，b2＝2b1＝－1，
b3＝－3b1＝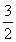
，bn＋3＝bn，
∴T1＝b1＝－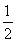
，T2＝T1b2＝
，
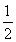T3＝T2b3＝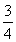
，T4＝T3b4＝T3b1＝
T1，
T5＝T4b5＝T2b3b4b5＝T2b1b2b3＝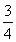
T2，
T6＝T5b6＝T3b4b5b6＝T3b1b2b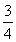3＝
T3，
……
T3n＋1＋T3n＋2＋T3n＋3＝T3n－2b3n－1b3nb3n＋1＋
T3n－1b3nb3n＋1b3n＋2＋T3nb3n＋1b3n＋2b3n＋3
＝T3n－2b1b2b3＋T3n－1b1b2b3＋T3nb1b2b3
＝
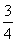(T3n－2＋T3n－1＋T3n)，
∴数列{T3n－2＋T3n－1＋T3n)(n∈N*)是等比数列，
首项T1＋T2＋T3＝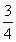
且公比q＝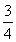
，(11分)记Sn＝T1＋T2＋T3＋…＋Tn，
①当n＝3k(k∈N*)时，
Sn＝(T1＋T2＋T3)＋(T4＋T5＋T6)…＋(T3k－2＋T3k－1＋T3k)
＝
，
∴
≤Sn＜3；(13分)
②当n＝3k－1(k∈N*)时
Sn＝(T1＋T2＋T3)＋(T4＋T5＋T6)＋…＋(T3k－2＋T3k－1＋T3k)－T3k
＝3
－(b1b2b3)k＝3－4·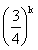
∴0≤Sn＜3；(14分)
③当n＝3k－2(k∈N*)时
Sn＝(T1＋T2＋T3)＋(T4＋T5＋T6)＋…＋(T3k－2＋T3k－1＋T3k)－T3k－1－T3k
＝3－(b1b2b3)k－1b1b2－
