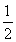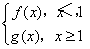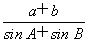题目内容
已知函数f(x)=x2+2ax+1(a∈R),f′(x)是f(x)的导函数.
(1)若x∈[-2,-1],不等式f(x)≤f′(x)恒成立,求a的取值范围;
(2)解关于x的方程f(x)=|f′(x)|; ?
(3)设函数g(x)=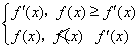 ,求g(x)在x∈[2,4]时的最小值.
,求g(x)在x∈[2,4]时的最小值.
(1)a≥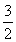 (2) x=1或x=-(1+2a) (3)4a+5
(2) x=1或x=-(1+2a) (3)4a+5
【解析】(1)因为f(x)≤f′(x),所以x2-2x+1≤2a(1-x),
又因为-2≤x≤-1, ?
所以a≥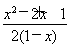 max在x∈[-2,-1]时恒成立,因为
max在x∈[-2,-1]时恒成立,因为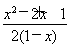 =
=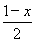 ≤
≤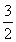 ,
,
所以a≥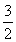 .(4分)
.(4分)
(2)因为f(x)=|f′(x)|,所以x2+2ax+1=2|x+a|,
所以(x+a)2-2|x+a|+1-a2=0,则|x+a|=1+a或|x+a|=1-a.(7分)
①当a<-1时,|x+a|=1-a,所以x=-1或x=1-2a;
②当-1≤a≤1时,|x+a|=1-a或|x+a|=1+a,
所以x=±1或x=1-2a或x=-(1+2a);
③当a>1时,|x+a|=1+a,所以x=1或x=-(1+2a).(10分)
(3)因为f(x)-f′(x)=(x-1)[x-(1-2a)],g(x)=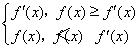
①若a≥-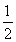 ,则x∈[2,4]时,f(x)≥f′(x),所以g(x)=f′(x)=2x+2a,
,则x∈[2,4]时,f(x)≥f′(x),所以g(x)=f′(x)=2x+2a,
从而g(x)的最小值为g(2)=2a+4;(12分)
②若a<-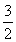 ,则x∈[2,4]时,f(x)<f′(x),所以g(x)=f(x)=x2+2ax+1,
,则x∈[2,4]时,f(x)<f′(x),所以g(x)=f(x)=x2+2ax+1,
当-2≤a<-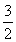 时,g(x)的最小值为g(2)=4a+5,
时,g(x)的最小值为g(2)=4a+5,
当-4<a<-2时,g(x)的最小值为g(-a)=1-a2,
当a≤-4时,g(x)的最小值为g(4)=8a+17.(14分)
③若-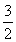 ≤a<-
≤a<-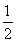 ,则x∈[2,4]时,
,则x∈[2,4]时,
g(x)=
当x∈[2,1-2a)时,g(x)最小值为g(2)=4a+5;
当x∈[1-2a,4]时,g(x)最小值为g(1-2a)=2-2a.
因为-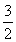 ≤a<-
≤a<-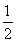 ,(4a+5)-(2-2a)=6a+3<0,
,(4a+5)-(2-2a)=6a+3<0,
所以g(x)最小值为4a+5,
综上所述,
[g(x)]min= (16分)
(16分)

 阅读快车系列答案
阅读快车系列答案