题目内容
【题目】等差数列{an}中，其前n项和为Sn ， 且 
，等比数列{bn}中，其前n项和为Tn ， 且 
，（n∈N*）
（1）求an ， bn；
（2）求{anbn}的前n项和Mn ．
【答案】
（1）解:法1：由 
，a1=1
又 
，所以a2=3或﹣1
因为a2=﹣1时， 
=1，故a2=﹣1舍去
所以等差数列{an）的公差d=a2﹣a1=2∴an=2n﹣1，
同样可得b1=1，b2=3或﹣1
因为b2=3时， 
，故b2=3舍去
又{bn}为等比数列，所以 
法2： ，a1=1…1分 
， 
，（n≥2）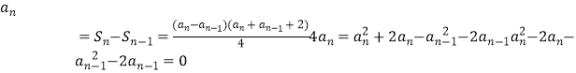 
（an﹣an﹣1）（an+an﹣1）﹣2（an+an﹣1）=0
（an﹣an﹣1﹣2）（an+an﹣1）=0，因为{an}为等差数列，
所以an﹣an﹣1﹣2=0，又a1=1∴an=2n﹣1，
又{bn}为等比数列，所以易得
（2）解：法一：Mn=a1b1+a2b2+…+anbn=1﹣3+5﹣7+…+（﹣1）n﹣1（2n﹣1）
若n为偶数，则Mn= 
所以Mn=﹣n
若n为奇数，则结合上边情况可得 Mn=﹣（n﹣1）+（2n﹣1）=n
综上可得Mn=（﹣1）n﹣1n
法二：Mn=1×（﹣1）0+3×（﹣1）1+5×（﹣1）2+…+（2n﹣1）×（﹣1）n﹣1…①
﹣Mn=1×（﹣1）1+3×（﹣1）2+5×（﹣1）3+…+（2n﹣1）×（﹣1）n…②
①﹣②得：
2Mn=1+2×（﹣1）1+2×（﹣1）2+2×（﹣1）3+…+2×（﹣1）n﹣1﹣（2n﹣1）×（﹣1）n
2Mn= 
Mn=n×（﹣1）n﹣1
【解析】（1）法1：利用等差数列的前3项求出公差与首项，再利用通项公式即可得出．法2：利用递推关系与等差数列的通项公式即可得出．（2）法1：利用分组求和即可得出．法2：利用“错位相减法”与等比数列的求和公式即可得出．
【考点精析】根据题目的已知条件，利用等差数列的通项公式（及其变式）和数列的前n项和的相关知识可以得到问题的答案，需要掌握通项公式：
或
；数列{an}的前n项和sn与通项an的关系
．
