题目内容
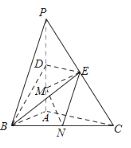
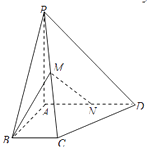
【题目】如图，在四棱柱ABCD﹣A1B1C1D1中，底面ABCD是等腰梯形，∠ADC=120°，AB=2CD=2，平面D1DCC1垂直平面ABCD，D1C⊥AB，M是线段AB的中点．
（Ⅰ）求证：D1M∥面B1BCC1；
（Ⅱ）若DD1=2，求平面C1D1M和平面ABCD所成的锐角的余弦值．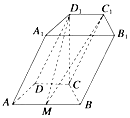
【答案】证明（Ⅰ）因为四边形ABCD是等腰梯形，且AB=2CD，所以AB∥DC．
又由M是AB的中点，因此CD∥MB且CD=MB．
在四棱柱ABCD﹣A1B1C1D1中，因为CD∥C1D1 ， CD=C1D1 ，
可得C1D1∥MB，C1D1=MB，所以四边形BMD1C1为平行四边形，
因此D1M∥BC1 ． 又D1M平面B1BCC1 ， BC1平面B1BCC1 ，
所以D1M∥平面B1BCC1
（Ⅱ）解：方法一：如图（2），连接AC，MC．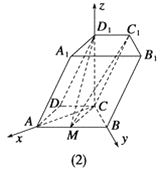
由（Ⅰ）知CD∥AM且CD=AM，
所以四边形AMCD为平行四边形，
可得BC=AD=MC，
由题意∠ABC=∠PAB=60°，
所以△MBC为正三角形，
因此AB=2BC=2，CA= 
，
因此CA⊥CB．
又D1C⊥AB，CD∥AB，故D1C⊥CD，而平面D1DCC1垂直平面ABCD且交于CD，则D1C⊥平面ABCD
以C为坐标原点，建立如图（2）所示的空间直角坐标系C﹣xyz
由DD1=2得D1C= ，所以A（ ，0，0），B（0，1，0），D1（0，0， ）
因此M 
，所以 
， 
设平面C1D1M的一个法向量为 
，
可得平面C1D1M的一个法向量 
又 
为平面ABCD的一个法向量
因此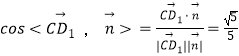 
所以平面C1D1M和平面ABCD所成的角（锐角）的余弦值为 
方法二：由（Ⅰ）知平面D1C1M∩平面ABCD=AB，过点C向AB引垂线交AB于点N，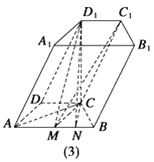
连接D1N，如图（3）．
由D1C⊥AB，CD∥AB，故D1C⊥CD，
而平面D1DCC1垂直平面ABCD且交于CD，
则D1C⊥平面ABCD，
可得D1N⊥AB，
因此∠D1NC为二面角C1﹣AB﹣C的平面角
在Rt△BNC中，BC=1，∠NBC=60°，可得CN= 
．
所以ND1= 
= 
．
在Rt△D1CN中，cos∠D1NC=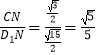 
，
所以平面C1D1M和平面ABCD所成的角（锐角）的余弦值为
【解析】（Ⅰ）证明AB∥DC．说明以四边形BMD1C1为平行四边形，推出D1M∥BC1 ． 然后证明D1M∥平面B1BCC1（Ⅱ）方法一连接AC，MC．以C为坐标原点，建立空间直角坐标系C﹣xyz，求出相关的坐标，求出平面C1D1M的一个法向量，平面ABCD的一个法向量，利用空间向量的数量积求解二面角的平面角的余弦函数值．方法二：说明∠D1NC为二面角C1﹣AB﹣C的平面角，通过在Rt△D1CN中，求解即可．
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能正确解答此题．
