题目内容
【题目】将圆x2+y2=1上每一点的纵坐标不变,横坐标变为原来的 ![]() ,得曲线C. (Ⅰ)写出C的参数方程;
,得曲线C. (Ⅰ)写出C的参数方程;
(Ⅱ)设直线l:3x+y+1=0与C的交点为P1、P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
【答案】解:(Ⅰ)∵将圆x2+y2=1上每一点的纵坐标不变,横坐标变为原来的 ![]() ,得曲线C. ∴由坐标变换公式
,得曲线C. ∴由坐标变换公式 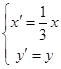 ,得x=3x′,y=y′,
,得x=3x′,y=y′,
代入x2+y2=1中,得9x'2+y'2=1,
故曲线C的参数方程为 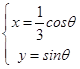 .(5分)
.(5分)
(Ⅱ)联立 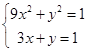 ,得
,得 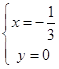 或
或 ![]() ,
,
由题知,P1(﹣ ![]() ,0),P2(0,﹣1),P1 P2线段中点M(﹣
,0),P2(0,﹣1),P1 P2线段中点M(﹣ ![]() ,﹣
,﹣ ![]() ),
),![]() =
= ![]() =﹣3,故P1 P2线段中垂线的方程为y+
=﹣3,故P1 P2线段中垂线的方程为y+ ![]() =
= ![]() (x+
(x+ ![]() ),(8分)
),(8分)
即3x﹣9y﹣4=0,即极坐标方程为3ρcosθ﹣9ρsinθ﹣4=0.(10分)
【解析】(Ⅰ)由坐标变换公式得x=3x′,y=y′,代入x2+y2=1中,得9x'2+y'2=1,由此能求出曲线C的参数方程.(Ⅱ)联立 ![]() ,得P1(﹣
,得P1(﹣ ![]() ,0),P2(0,﹣1),由此能求出过线段P1P2的中点且与l垂直的直线的极坐标方程.
,0),P2(0,﹣1),由此能求出过线段P1P2的中点且与l垂直的直线的极坐标方程.

练习册系列答案
相关题目