题目内容
已知 ,不等式
,不等式 的解集为
的解集为 .
.
(1)求 的值;
的值;
(2)若 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数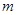 的取值范围.
的取值范围.
 ,不等式
,不等式 的解集为
的解集为 .
.(1)求
 的值;
的值;(2)若
 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数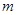 的取值范围.
的取值范围.(1)2;(2) .
.
 .
.试题分析:(1)我们首先求出不等式
 的解集,这个解集与
的解集,这个解集与 相等,由此可求得
相等,由此可求得 ;(2)
;(2) ,一种方法,这个函数是分段函数,我们把它化为一般的分段函数表达式,以便求出它的最大(小)值,从而求得
,一种方法,这个函数是分段函数,我们把它化为一般的分段函数表达式,以便求出它的最大(小)值,从而求得 的最大值,得到
的最大值,得到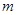 的取值范围,也可应用绝对值不等式的性质
的取值范围,也可应用绝对值不等式的性质 ,求得最大值.
,求得最大值.试题解析:解法一:(1)由不等式|2x-a|-a≤2,得|2x-a|≤2+a,
∵解集不空,∴2+a≥0.
解不等式可得{x∣-1≤x≤1+a}. 3分
∵-1≤x≤3,∴1+a﹦3,即a=2. 5分
(2)记g(x)=f(x)-f(x+2)=|2x-2|-|2x+2|, 6分
4,(x≤-1)
则g(x)= -4x,(-1﹤x﹤1). 8分
-4,(x≥1)
所以-4≤g(x)≤4,∴|g(x)|≤4,因此m≥4. 10分
解法二:∵f(x)-f(x+2)=|2x-2|-|2x+2|,
∵|2x-2|-|2x+2|≤|(2x-2)-(2x+2)|=4. 7分
|2x-2|-|2x+2|≥|2x|-2-(|2x|+2)=-4. 9分
∴-4≤|2x-2|-|2x+2|≤4.
∴|f(x)-f(x+2)|≤4.
∴m≥4. 10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 时,解不等式
时,解不等式 ;
; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.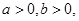 且
且 ,若
,若 恒成立,
恒成立, 的最小值;(2)若
的最小值;(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. +
+ +…+
+…+ <
< .
. ,则两边均含有运算“*”和“+”,且对任意3个实数a,b,c都能成立的一个等式可以是 .
,则两边均含有运算“*”和“+”,且对任意3个实数a,b,c都能成立的一个等式可以是 . ,若“
,若“ ”是“
”是“ ”的充分条件,则
”的充分条件,则 的取值范围是( )
的取值范围是( )



 在
在 时恒成立,则实数
时恒成立,则实数 的取值范围是__________.
的取值范围是__________. ,则f(10x)>0的解集为______.
,则f(10x)>0的解集为______.