题目内容
设定义域为R的函数，f(x)=
，关于x的方程f2（x）-（2m+1）f（x）+m2=0有7个不同的实数解，则m的值为（ ）
|
分析：作出函数f（x）的图象，由图象判断要使方程f2（x）-（2m+1）f（x）+m2=0有7个不同的实数根，即要求对应于f（x）的取值即可求出m的值．
解答：解：设f（x）=t，作出函数f（x）的图象，由图象可知，
当t＞4时，函数图象有两个交点，
当t=4时，函数图象有3个交点，
当0＜t＜4时，函数图象有4个交点，
当t=0时，函数图象有两个交点，
当t＜0，函数图象无交点．
要使原方程f2（x）-（2m+1）f（x）+m2=0有7个不同的实数根，
则要求对应方程t2-（2m+1）t+m2=0中的两个根t1=4或0＜t2＜4，
且t1+t2∈（4，8），即4＜2m+1＜8，解得
＜m＜
．
当t=4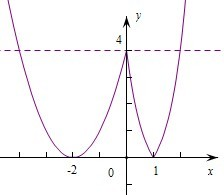
时，它有三个根．
∴42-4（2m+1）+m2=0，
∴m=2或m=6（舍去），
∴m=2．
故选A．
当t＞4时，函数图象有两个交点，
当t=4时，函数图象有3个交点，
当0＜t＜4时，函数图象有4个交点，
当t=0时，函数图象有两个交点，
当t＜0，函数图象无交点．
要使原方程f2（x）-（2m+1）f（x）+m2=0有7个不同的实数根，
则要求对应方程t2-（2m+1）t+m2=0中的两个根t1=4或0＜t2＜4，
且t1+t2∈（4，8），即4＜2m+1＜8，解得
| 3 |
| 2 |
| 7 |
| 2 |
当t=4
时，它有三个根．∴42-4（2m+1）+m2=0，
∴m=2或m=6（舍去），
∴m=2．
故选A．
点评：本题主要考查复合函数的根的取值判断，利用数形结合作出函数f（x）的图象是解决本题的关键，综合性较强．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
设定义域为R的函数f（x）满足下列条件：①对任意x∈R，f（x）+f（-x）=0；②对任意x1，x2∈[1，a]，当x2＞x1时，有f（x2）＞f（x1）＞0．则下列不等式不一定成立的是（ ）
| A、f（a）＞f（0） | ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|
设定义域为R的函数f（x）=