题目内容
设x,y,z都是正实数,a=x+ ,b=y+
,b=y+ ,c=z+
,c=z+ ,则a,b,c三个数( ).
,则a,b,c三个数( ).
| A.至少有一个不大于2 | B.都小于2 |
| C.至少有一个不小于2 | D.都大于2 |
C
解析试题分析:将三个式子相加,构造出均值不等式的形式,由均值不等式可得a+b+c≥6,从而推出a,b,c的范围.因为x,y,z都是正实数,a=x+ ,b=y+
,b=y+ ,c=z+
,c=z+ ,那么可知a+b+c=
,那么可知a+b+c=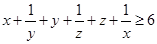 ∴a,b,c至少有一个不小于2.故选C.
∴a,b,c至少有一个不小于2.故选C.
考点:基本不等式
点评:基本不等式是高考重点考查的知识点之一,应用基本不等式时,要熟练掌握不等式成立的条件与重要不等式的变形.

练习册系列答案
相关题目
对于实数 和
和 ,定义运算
,定义运算 :
: ,若对任意
,若对任意 ,不等式
,不等式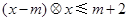 都成立,则实数
都成立,则实数 的取值范围是
的取值范围是
A. | B.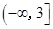 |
C.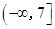 | D. |
已知 ,且
,且 ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
若a>1, 则  的最小值是 ( )
的最小值是 ( )
| A.2 | B.4 | C.1 | D.3 |
若 ,且
,且 ,则下列不等式中,恒成立的是 ( )
,则下列不等式中,恒成立的是 ( )
A. | B. |
C. | D. |
若 且2
且2 =2,则
=2,则 的最小值是( )
的最小值是( )
| A.2 | B. | C. | D. |
函数 的图像恒过定点A,若点A在直线
的图像恒过定点A,若点A在直线 上,其中mn>0,则
上,其中mn>0,则 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.4 |
设 ,且
,且 ,则四个数
,则四个数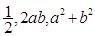 ,b中最大的是
,b中最大的是
A. | B. | C. | D. |
 ,得2分的概率为
,得2分的概率为 ,不得分的概率为
,不得分的概率为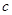 ,
, ,已知他投篮一次得分的期望是2,则
,已知他投篮一次得分的期望是2,则 的最小值为( )
的最小值为( )


