题目内容
函数 的图像恒过定点A,若点A在直线
的图像恒过定点A,若点A在直线 上,其中mn>0,则
上,其中mn>0,则 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:由题意可得函数 的图像恒过定点A(1,1),又点A在直线mx+ny-2=0=0上,
的图像恒过定点A(1,1),又点A在直线mx+ny-2=0=0上,
∴m+n=2,∴ =
= ,当且仅当
,当且仅当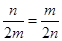 ,时取“=”可得m=n=1,所以
,时取“=”可得m=n=1,所以 的最小值为2,故选B
的最小值为2,故选B
考点:本题考查了基本不等式的应用
点评:基本不等式是求解二元最值问题的常用方法,本题用到了“1”的代换及函数图象过定点问题,解题过程中用到了转化的思想,是一道基础题

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
已知 ,以下三个结论:①
,以下三个结论:① ,②
,② ③
③ ,其中正确的个数是( )
,其中正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
设x,y,z都是正实数,a=x+ ,b=y+
,b=y+ ,c=z+
,c=z+ ,则a,b,c三个数( ).
,则a,b,c三个数( ).
| A.至少有一个不大于2 | B.都小于2 |
| C.至少有一个不小于2 | D.都大于2 |
若对于使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最小值
的最小值 叫做
叫做 的上确界,若
的上确界,若 ,则
,则 的上确界是( )
的上确界是( )
A. | B.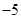 | C. | D.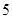 |
若a <0,则a + ( )
( )
| A.有最小值2 | B.有最大值2 |
| C.有最小值-2 | D.有最大值-2 |
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.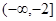 | B. | C. | D. |
若三点 (2,2),
(2,2),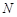 (
( ,0),
,0), (0,
(0,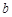 ),(
),( )共线,则
)共线,则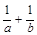 的值为( )
的值为( )
| A.1 | B. | C. | D. |
若 ,则
,则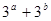 的最小值( )
的最小值( )
| A.4 | B.5 | C.6 | D.7 |
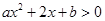 解集为
解集为 且
且 ,则
,则 的最小值为 .
的最小值为 .