题目内容
对于实数 和
和 ,定义运算
,定义运算 :
: ,若对任意
,若对任意 ,不等式
,不等式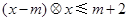 都成立,则实数
都成立,则实数 的取值范围是
的取值范围是
A. | B.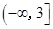 |
C.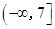 | D. |
C
解析试题分析:由新定义,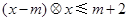 即,
即, ,亦即
,亦即 ,在
,在 时恒成立,而
时恒成立,而 ,
,
故实数 的取值范围是
的取值范围是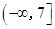 ,选C。
,选C。
考点:均值定理的应用,新定义问题。
点评:中档题,新定义问题,关键是理解其意义,转化得到具体不等式恒成立,利用均值定理,研究函数的最值,进一步求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的最小值是( )
的最小值是( )
| A.2 | B. | C.5 | D.8 |
若 在直线上
在直线上 移动,则
移动,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
已知 ,以下三个结论:①
,以下三个结论:① ,②
,② ③
③ ,其中正确的个数是( )
,其中正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
下列不等式中正确的是
A. |
B. |
C. |
D. |
若 ,且
,且 .则
.则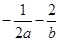 的最大值是( )
的最大值是( )
A.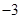 | B. | C.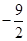 | D. |
已知正数 满足
满足 则
则 的最小值为( )
的最小值为( )
A. | B.4 | C. | D. |
设x,y,z都是正实数,a=x+ ,b=y+
,b=y+ ,c=z+
,c=z+ ,则a,b,c三个数( ).
,则a,b,c三个数( ).
| A.至少有一个不大于2 | B.都小于2 |
| C.至少有一个不小于2 | D.都大于2 |
若三点 (2,2),
(2,2),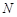 (
( ,0),
,0), (0,
(0,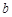 ),(
),( )共线,则
)共线,则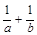 的值为( )
的值为( )
| A.1 | B. | C. | D. |