题目内容
【题目】已知在平面直角坐标系
中，圆
的参数方程为
（
为参数）．以原点
为极点，
轴的非负半轴为极轴，取相同的单位长度建立极坐标系．
（1）求圆的普通方程及其极坐标方程；
（2）设直线
的极坐标方程为
，射线
与圆的交点为
（异于极点），与直线的交点为
，求线段
的长．
【答案】(1) 普通方程为：
; 极坐标方程为：
．(2) 
【解析】
（1）由圆的参数方程消去参数，得到普通方程，再由直角坐标与极坐标的互化公式，得到极坐标方程；
（2）将
代入圆的极坐标方程，得到
；将代入直线
的极坐标方程，得到
，再由
，即可得出结果.
（1）由
平方相加，得：，
所以圆
的普通方程为：
又
，
，∴
化简得圆的极坐标方程为：．
（2）把代入圆的极坐标方程可得：
把代入直线的极坐标方程可得：
， ∴
所以线段
的长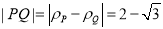
练习册系列答案
阅读快车系列答案
相关题目
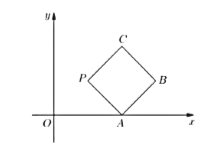
【题目】如图所示，在平面直角坐标系
上放置一个边长为1的正方形
，此正方形沿
轴滚动（向左或者向右均可），滚动开始时，点
在原点处，例如：向右滚动时，点的轨迹起初时以点
为圆心，1为半径的
圆弧，然后以点
与轴交点为圆心，
长度为半径……，设点
的纵坐标与横坐标的函数关系式是
，该函数相邻两个零点之间的距离为
.
（1）写出的值，并求出当
时，点轨迹与轴所围成的图形的面积
，研究该函数的性质并填写下面的表格：
函数性质 | 结论 | |
奇偶性 | ||
单调性 | 递增区间 | |
递减区间 | ||
零点 | ||
（2）已知方程
在区间
上有11个根，求实数
的取值范围
（3）写出函数
的表达式.