题目内容
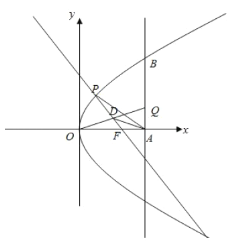
【题目】如图,![]() 是等边三角形,
是等边三角形, ![]() 是
是![]() 边上的动点(含端点),记
边上的动点(含端点),记![]() ,
,![]() .
.

(1)求![]() 的最大值;
的最大值;
(2)若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)当α=![]() ,即D为BC中点时,原式取最大值
,即D为BC中点时,原式取最大值![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可得β=α+![]() ,根据三角函数和差公式及辅助角公式化简即可求出其最大值。
,根据三角函数和差公式及辅助角公式化简即可求出其最大值。
(2)根据三角函数差角公式求得sinα,再由正弦定理,求得AB的长度;进而求得三角形面积。
(1)由△ABC是等边三角形,得β=α+![]() ,
,
0≤α≤![]() ,故2cos
,故2cos![]() -cos
-cos![]() =2cos
=2cos![]() -cos
-cos![]() =
=![]() sin
sin![]() ,
,
故当α=![]() ,即D为BC中点时,原式取最大值
,即D为BC中点时,原式取最大值![]()
(2)由cos β=![]() ,得sin β=
,得sin β=![]() ,
,
故sin α=sin![]() =sin βcos
=sin βcos![]() -cos βsin
-cos βsin![]() =
=![]() ,
,
由正弦定理![]() ,
,
故AB=![]() BD=
BD=![]() ×1=
×1=![]() ,故S△ABD=
,故S△ABD=![]() AB·BD·sin B=
AB·BD·sin B=![]()

【题目】有一名高二学生盼望2020年进入某名牌大学学习,假设该名牌大学有以下条件之一均可录取:①2020年2月通过考试进入国家数学奥赛集训队(集训队从2019年10月省数学竞赛一等奖中选拔):②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线,③2020年6月高考达到该校录取分数线(该校录取分数线高于重点线),该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
省数学竞赛一等奖 | 自主招生通过 | 高考达重点线 | 高考达该校分数线 |
0.5 | 0.6 | 0.9 | 0.7 |
若该学生数学竞赛获省一等奖,则该学生估计进入国家集训队的概率是0.2.若进入国家集训队,则提前录取,若未被录取,则再按②、③顺序依次录取:前面已经被录取后,不得参加后面的考试或录取.(注:自主招生考试通过且高考达重点线才能录取)
(Ⅰ)求该学生参加自主招生考试的概率;
(Ⅱ)求该学生参加考试的次数![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)求该学生被该校录取的概率.
【题目】某地1~10岁男童年龄![]() (单位:岁)与身高的中位数
(单位:岁)与身高的中位数![]() (单位
(单位![]() ,如表所示:
,如表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 76.5 | 88.5 | 96.8 | 104.1 | 111.3 | 117.7 | 124 | 130 | 135.4 | 140.2 |
对上表的数据作初步处理,得到下面的散点图及一些统计量的值.
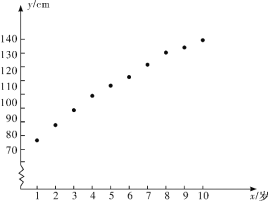
|
|
|
|
112.45 | 82.50 | 3947.71 | 566.85 |
(1)求![]() 关于
关于![]() 的线性回归方程(回归方程系数精确到0.01);
的线性回归方程(回归方程系数精确到0.01);
(2)某同学认为方程![]() 更适合作为
更适合作为![]() 关于
关于![]() 的回归方程模型,他求得的回归方程是
的回归方程模型,他求得的回归方程是![]() .经调查,该地11岁男童身高的中位数为
.经调查,该地11岁男童身高的中位数为![]() ,与(1)中的线性回归方程比较,哪个回归方程的拟合效果更好?
,与(1)中的线性回归方程比较,哪个回归方程的拟合效果更好?
(3)从6岁~10岁男童中每个年龄阶段各挑选一位男童参加表演(假设该年龄段身高的中位数就是该男童的身高).再从这5位男童中任挑选两人表演“二重唱”,则“二重唱”男童身高满足![]() 的概率是多少?
的概率是多少?
参考公式: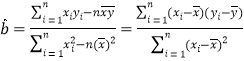 ,
,![]()