Question

【题目】已知函数．

（1）若函数f（x）在（0，+∞）上是减函数，其实数m的取值范围；

（2）若函数f（x）在（0，+∞）上存在两个极值点x1，x2，证明：lnx1+lnx2＞2．

Answer 1

【答案】（1）．（2）证明见解析

【解析】

(1)由题知在上恒成立.参变分离求实数m的取值范围即可.

(2)求导代入极值点分析满足的关系式,再代换构造出关于的方程,再换元证明不等式即可.

（1）由函数f（x）在（0,+∞）上是减函数,可知,f′（x）＝lnx﹣mx≤0恒成立,

∴m恒成立,故mmax,

令g（x）,x＞0,

则g′（x）,

当x∈（0,e）,g′（x）0,g（x）单调递增,

当x∈（e,+∞）,则g′（x）0,g（x）单调递减,

g（x）max＝g（e）,

∴．

（2）由（1）f′（x）＝lnx﹣mx,

由f（x）在（0,+∞）上存在两个极值点,不妨设x1＜x2,

知,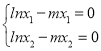

则m,

又m,

∴,

即lnx1+lnx2,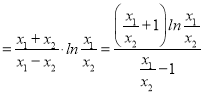

设t∈（0,1）,

要证明：lnx1+lnx2＞2,

只要证,

只要证lnt,

即证lnt0,

构造函数h（t）＝lnt,

h′（t）0,

h（t）在（0,1）上单调递增,

∴h（t）＜h（1）＝0,

即h（t）＝lnt0,

∴lnx1+lnx2＞2．