题目内容
((本小题满分14分)
已知函数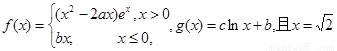 是函数
是函数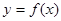 的极值点。
的极值点。
(Ⅰ)当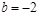 时,求a的值,讨论函数
时,求a的值,讨论函数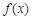 的单调性;
的单调性;
(Ⅱ)当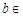 R时,函数
R时,函数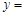
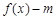 有两个零点,求实数m的取值范围.
有两个零点,求实数m的取值范围.
(Ⅲ)是否存在这样的直线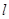 ,同时满足:
,同时满足:
①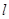 是函数
是函数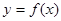 的图象在点
的图象在点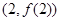 处的切线
处的切线
②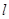
 与函数
与函数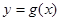 的图象相切于点
的图象相切于点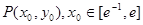 ,
,
如果存在,求实数b的取值范围;不存在,请说明理由。
解:(1)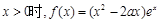 ,
,
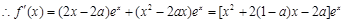 . ....1分
. ....1分
由已知得,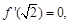
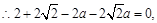 解得a=1.
……2分
解得a=1.
……2分
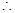
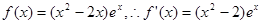 .
.
当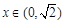 时,
时,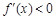 ,当
,当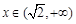 时,
时,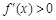 .又
.又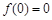 , ....3分
, ....3分
当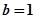 时,
时,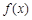 在
在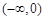 ,
,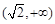 上单调递增,在
上单调递增,在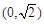 上单调递减. ………4分
上单调递减. ………4分
(2)由(1)知,当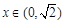 时,
时,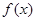 单调递减,
单调递减,
当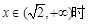 ,
,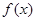 单调递增,
单调递增,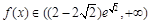 . ………………2分
. ………………2分
要使函数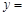
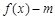 有两个零点,则函数
有两个零点,则函数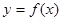 的图象与直线
的图象与直线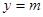 有两个不同的交点.
有两个不同的交点.
①当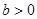 时,m=0或
时,m=0或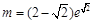 ;
....3分
;
....3分
②当b=0时,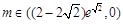 ;
....4分
;
....4分
③当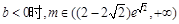 . ..
. .. ..5分
..5分
(3)假设存在, 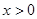 时,
时,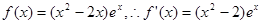
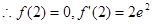
函数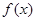 的图象在点
的图象在点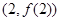 处的切线
处的切线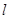 的方程为:
的方程为: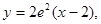 ....1分
....1分
 直线
直线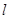 与函数
与函数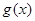 的图象相切于点
的图象相切于点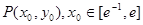 ,
,
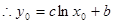 ,
,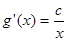 ,所以切线
,所以切线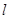 的斜率为
的斜率为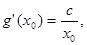
所以切线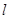 的方程为
的方程为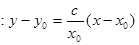
即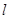 的方程为:
的方程为: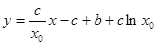 …………2分
…………2分
得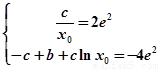
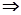
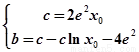
得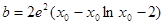 其中
其中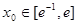 ....3分
....3分
记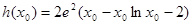 其中
其中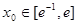
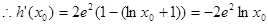
令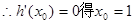 ....4分
....4分
|
|
|
1 |
|
|
|
+ |
0 |
- |
|
|
|
极大值 |
|
又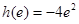 ,
,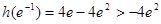
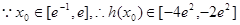
所以实数b的取值范围的集合: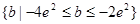 …………5分
…………5分
【解析】略

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
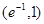
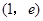
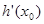
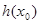
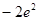

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)