题目内容
【题目】已知函数![]()
(1)若![]() ,是否存在
,是否存在![]() ,使得
,使得![]() 为偶函数,如果存在,请举例并证明,如果不存在,请说明理由;
为偶函数,如果存在,请举例并证明,如果不存在,请说明理由;
(2)若![]() ,判断
,判断![]() 在
在![]() 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(3)已知![]() ,存在
,存在![]() ,对任意
,对任意![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;
(2)见解析;
(3)![]() .
.
【解析】
(1)将![]() 代入证明
代入证明![]() 为偶函数即可。
为偶函数即可。
(2)代入![]() ,先判断函数为单调递减函数,再根据定义法代入作差即可证明
,先判断函数为单调递减函数,再根据定义法代入作差即可证明![]() 为单调递减函数。
为单调递减函数。
(3)去绝对值化简不等式,根据全称命题与特称命题的成立关系可得![]() ,分两段不等式求解即可。
,分两段不等式求解即可。
(1)存在![]() 使
使![]() 为偶函数,
为偶函数,
此时:![]() ,
,
证明:![]() 的定义域为
的定义域为![]() 关于原点对称,
关于原点对称,
且![]()
![]() 为偶函数。
为偶函数。
(2)![]() ,且
,且![]() ,
,![]() ,
,
![]() 在
在![]() 上为减函数
上为减函数
证明:任取![]() ,且
,且![]() ,
,
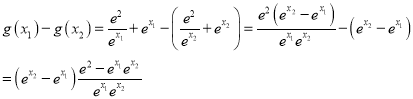
![]()
![]() ,即
,即![]()
![]() 在
在![]() 上为减函数
上为减函数
(3)![]() ,
,![]() ,
,
![]() 对任意
对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,
成立,
即存在![]() ,使得
,使得![]() ,
,
当![]() 时,
时,![]() 为增函数或常函数,
为增函数或常函数,
![]()
此时![]() ,则有
,则有![]() 恒成立
恒成立
当![]() 时,
时,![]()
![]()
![]()
![]()
![]()
![]()
当![]() 时,
时,![]()
![]()
![]()
![]()
![]()
![]()
综上所述:. ![]()

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,杨老师的微信朋友圈内有
推出的多款健康运动软件中的一款,杨老师的微信朋友圈内有![]() 位好友参与了“微信运动”,他随机选取了
位好友参与了“微信运动”,他随机选取了![]() 位微信好友(女
位微信好友(女![]() 人,男
人,男![]() 人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
5860 8520 7326 6798 7325 8430 3216 7453 11754 9860
8753 6450 7290 4850 10223 9763 7988 9176 6421 5980
男性好友走路的步数情况可分为五个类别: ![]() 步)(说明:“
步)(说明:“![]() ”表示大于等于
”表示大于等于![]() ,小于等于
,小于等于![]() .下同),
.下同), ![]() 步),
步), ![]() 步),
步), ![]() 步),
步), ![]() 步及以
步及以![]() ),且
),且![]() 三种类别人数比例为
三种类别人数比例为![]() ,将统计结果绘制如图所示的条形图.
,将统计结果绘制如图所示的条形图.

若某人一天的走路步数超过![]() 步被系统认定为“卫健型",否则被系统认定为“进步型”.
步被系统认定为“卫健型",否则被系统认定为“进步型”.
(1)若以杨老师选取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计杨老师的微信好友圈里参与“微信运动”的![]() 名好友中,每天走路步数在
名好友中,每天走路步数在![]() 步的人数;
步的人数;
(2)请根据选取的样本数据完成下面的![]() 列联表并据此判断能否有
列联表并据此判断能否有![]() 以上的把握认定“认定类型”与“性别”有关?
以上的把握认定“认定类型”与“性别”有关?
| p> | 卫健型 | 进步型 | 总计 |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
(3)若从杨老师当天选取的步数大于10000的好友中按男女比例分层选取![]() 人进行身体状况调查,然后再从这
人进行身体状况调查,然后再从这![]() 位好友中选取
位好友中选取![]() 人进行访谈,求至少有一位女性好友的概率.
人进行访谈,求至少有一位女性好友的概率.
附:  ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |