��Ŀ����
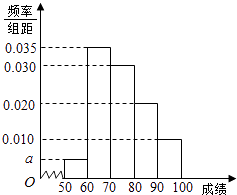
����Ŀ��ijУ100��ѧ�����п�����ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ�����гɼ������������£�
��� | ��һ�� | �ڶ��� | ������ | ������ | ������ |
���� | [50��60�� | [60��70�� | [70��80�� | [80��90�� | [90��100] |
������ͼ��a��ֵ��
������Ƶ�ʷֲ�ֱ��ͼ��������100��ѧ�����п�����ѧ�ɼ���ƽ���֣�
�������÷ֲ�����ķ����ӵ�3��4��5���������ȡ6��ѧ����������������һ�����壬���������ȡ2����������ǡ��1�˵ķ���������90�ֵĸ��ʣ�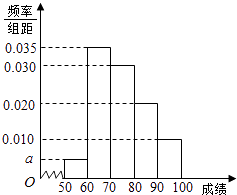
���𰸡��⣺�����������10a+0.01��10+0.02��10+0.03��10+0.035��10=1������a=0.005�� ������ֱ��ͼ������[50��60]��Ƶ��Ϊ0.05��[60��70]��Ƶ��Ϊ0.35��[70��80]��Ƶ��Ϊ0.30��
[80��90]��Ƶ��Ϊ0.20��[90��100]��Ƶ��Ϊ0.10��������100��ѧ�����п�����ѧ�ɼ���ƽ���ֵĹ���ֵΪ��55��0.05+65��0.35+75��0.30+85��0.20+95��0.10=74.5
������ֱ��ͼ���ã�
��3������Ϊ0.3��100=30��
��4������Ϊ0.2��100=20�ˣ�
��5������Ϊ0.1��100=10�ˣ�
�������÷ֲ������60��ѧ���г�ȡ6��ѧ����
ÿ��ֱ�Ϊ��
��3�飺 ![]() �ˣ�
�ˣ�
��4�飺 ![]() �ˣ�
�ˣ�
��5�飺 ![]() =1�ˣ�
=1�ˣ�
���Ե�3��4��5��ֱ��ȡ3�ˡ�2�ˡ�1�ˣ�
���3���3λͬѧΪA1 �� A2 �� A3 �� ��4���2λͬѧΪB1 �� B2 �� ��5���1λͬѧΪC1 �� �����λͬѧ�г���λͬѧ��15�ֿ������£�
��A1 �� A2������A1 �� A3������B1 �� B2������A2 �� A3������A1 �� B1������A1 �� B2������A2 �� B1������A2 �� B2������A3 �� B1������A3 �� B2������A1 �� C1������A2 �� C1������A3 �� C1������B1 �� C1������B2 �� C1����
����ǡ��1�˵ķ���������90���֣��������У���A1 �� C1������A2 �� C1������A3 �� C1������B1 �� C1������B2 �� C1������5�֣�
�������е�4���2λͬѧ������һλͬѧ��ѡ�ĸ���Ϊ ![]()
����������1���������Ը��ʵĺ�Ϊ1����������ε������Ϊ1��������ʽ��ϵ�����������2����ֵΪ��������ֵ�����Ƶ��֮���ĺͣ���3���ȷֱ����3��4��5��������������ùŵ����֪ʶ��⣮

 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�