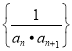题目内容
【题目】某家庭进行理财投资,根据长期收益率市场调查和预测,投资债券等稳键型产品A的收益与投资成正比,其关系如图1所示;投资股票等风险型产品B的收益与投资的算术平方根成正比,其关系如图2所示(收益与投资单位:万元). 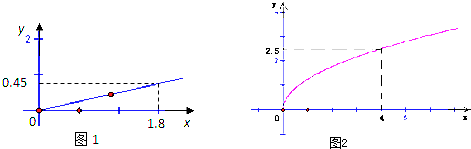
(1)分别将A、B两种产品的收益表示为投资的函数关系式;
(2)该家庭现有10万元资金,并全部投资债券等稳键型产品A及股票等风险型产品B两种产品,问:怎样分配这10万元投资,才能使投资获得最大收益,其最大收益为多少万元?
【答案】
(1)解:设投资为x万元,
A、B两产品获得的收益分别为f(x)、g(x)万元,
由题意,f(x)=k1x,g(x)= ![]() ,k1,k2≠0,x≥0,
,k1,k2≠0,x≥0,
又由图知f(1.8)=0.45,g(4)=2.5;解得 ![]() ,k2=
,k2= ![]() ,
,
∴f(x)= ![]() ,x≥0.g(x)=
,x≥0.g(x)= ![]()
(2)解:设对股票等风险型产品B投资x万元,则对债券等稳键型产品A投资(10﹣x)万元,
记家庭进行理财投资获取的收益为y万元,
则y= ![]() ,x≥0.
,x≥0.
设 ![]() ,则x=t2,0≤t≤
,则x=t2,0≤t≤ ![]() .
.
∴y=﹣ ![]() ,
,
当t= ![]() ,也即x=
,也即x= ![]() 时,y取最大值
时,y取最大值 ![]() .
.
答:对股票等风险型产品B投资 ![]() 万元,对债券等稳键型产品A投资
万元,对债券等稳键型产品A投资 ![]() 万元时,
万元时,
可获最大收益 ![]() 万元
万元
【解析】(1)设投资为x万元,A、B两产品获得的收益分别为f(x)、g(x)万元,由题意,f(x)=k1x,g(x)= ![]() ,k1 , k2≠0,x≥0,再由图象能求出A、B两种产品的收益表示为投资的函数关系式.(2)设对股票等风险型产品B投资x万元,则对债券等稳键型产品A投资(10﹣x)万元,记家庭进行理财投资获取的收益为y万元,则y=
,k1 , k2≠0,x≥0,再由图象能求出A、B两种产品的收益表示为投资的函数关系式.(2)设对股票等风险型产品B投资x万元,则对债券等稳键型产品A投资(10﹣x)万元,记家庭进行理财投资获取的收益为y万元,则y= ![]() ,x≥0.利用换元法能求出怎样分配这10万元投资,才能使投资获得最大收益,并能求出其最大收益为多少万元.
,x≥0.利用换元法能求出怎样分配这10万元投资,才能使投资获得最大收益,并能求出其最大收益为多少万元.

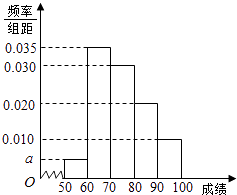
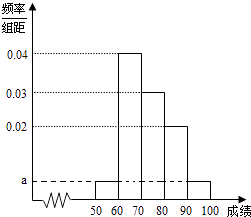
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(Ⅰ)求图中a的值;
(Ⅱ)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(Ⅲ)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?