题目内容
【题目】定义在![]() 上的函数
上的函数![]() ,恒有
,恒有![]() 成立,且
成立,且![]() ,对任意的
,对任意的![]() ,则
,则![]() 成立的充要条件是( )
成立的充要条件是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】由f(x)=f(2﹣x),得函数关于x=1对称,
由f'(x)(x﹣1)>0得,
当x>1时,f′(x)>0,此时函数为增函数,
当x<1时,f′(x)<0,此时函数f(x)为减函数,
若x1<x2,当x2≤1,函数为减函数,满足对任意的x1<x2,f(x1)>f(x2),
此时x1+x2<2,若x2>1,∵函数f(x)关于x=1对称,则f(x2)=f(2﹣x2),
则2﹣x2<1,则由f(x1)>f(x2)得f(x1)>f(x2)=f(2﹣x2),
此时函数在x<1时为减函数,则x1<2﹣x2,即x1+x2<2,
即对任意的x1<x2,f(x1)>f(x2)得x1+x2<2,反之也成立,
即对任意的x1<x2,f(x1)>f(x2)是x1+x2<2的充要条件,
故选:B

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
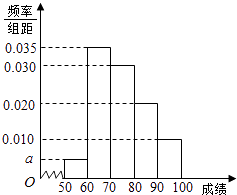
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(Ⅰ)求图中a的值;
(Ⅱ)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(Ⅲ)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?