题目内容
【题目】已知函数f（x）=2cos2ωx+2sinωxcosωx（ω＞0）的最小正周期为π．
（1）求f（ 
）的值；
（2）求函数f（x）的单调递增区间．
【答案】
（1）解：函数f（x）=2cos2ωx+2sinωxcosωx=cos2ωx+sin2ωx+1= 
sin（2ωx+ 
）+1，
因为f（x）最小正周期为π，所以 
=π，解得ω=1，
所以f（x）= sin（2x+ ）+1，
f（ 
）= sin（ 
+ ）+1= （sin cos +cos sin ）+1= 
（2）解：由2kπ﹣ 
≤2x+ ≤2kπ+ ，可得 kπ﹣ 
≤x≤kπ+ 
，
所以，函数f（x）的单调递增区间为[kπ﹣ ，kπ+ ]，k∈Z
【解析】（1）利用三角恒等变换化简函数的解析式，再利用正弦函数的周期性求得ω的值，可得函数的解析式．（2）利用正弦函数的单调性求得函数f（x）的单调递增区间．
练习册系列答案
阅读快车系列答案
相关题目
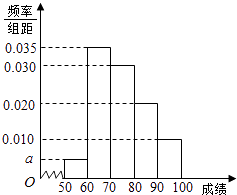
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
（Ⅰ）求图中a的值；
（Ⅱ）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；
（Ⅲ）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？
