题目内容
(本小题满分14分)
设等差数列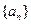 前
前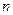 项和为
项和为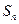 ,则有以下性质:
,则有以下性质: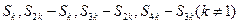 成等差数列.
成等差数列.
(1) 类比等差数列的上述性质,写出等比数列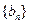 前
前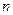 项积
项积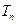 的类似性质;
的类似性质;
(2) 证明(1)中所得结论.
设等差数列
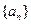 前
前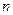 项和为
项和为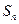 ,则有以下性质:
,则有以下性质: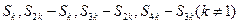 成等差数列.
成等差数列. (1) 类比等差数列的上述性质,写出等比数列
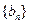 前
前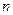 项积
项积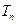 的类似性质;
的类似性质;(2) 证明(1)中所得结论.
(本小题满分14分)
(1)
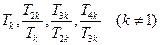 成等比数列.
成等比数列.
(2)证明
(1)
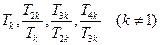 成等比数列.
成等比数列. (2)证明
(本小题满分14分)
解:(1)若设等比数列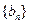 的前
的前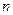 项积为
项积为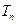 ,则
,则
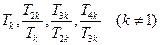 成等比数列. ---------4分
成等比数列. ---------4分
(2)证明: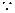 等比数列
等比数列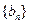 的前
的前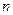 项积为
项积为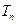 ,设公比为
,设公比为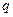 ,
,
∴ ,
, 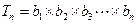 ----------------5分
----------------5分
∴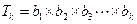 . -------------6分
. -------------6分
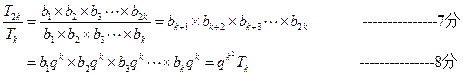
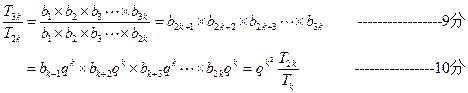
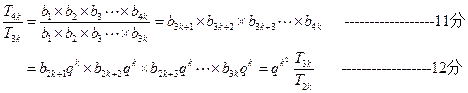
∵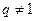 , ∴
, ∴ 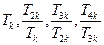 成等比数列 ---------------------------14分
成等比数列 ---------------------------14分
解:(1)若设等比数列
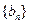 的前
的前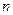 项积为
项积为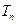 ,则
,则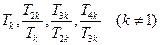 成等比数列. ---------4分
成等比数列. ---------4分(2)证明:
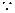 等比数列
等比数列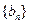 的前
的前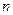 项积为
项积为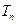 ,设公比为
,设公比为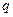 ,
,∴
 ,
, 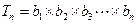 ----------------5分
----------------5分∴
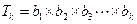 . -------------6分
. -------------6分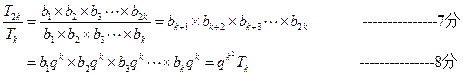
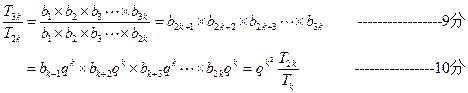
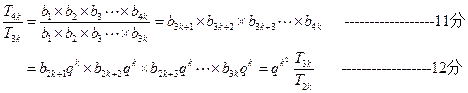
∵
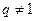 , ∴
, ∴ 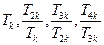 成等比数列 ---------------------------14分
成等比数列 ---------------------------14分
练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
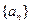 的前
的前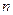 项和为
项和为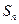 ,点
,点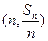 在直线
在直线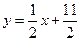 上;数列
上;数列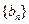 满足
满足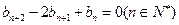 ,且
,且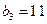 ,它的前9项和为153.
,它的前9项和为153.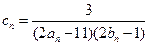 ,求数列
,求数列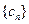 的前
的前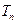 .
.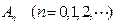 ,其中
,其中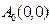 ,
,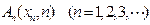 ,并且线段
,并且线段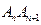 所在直线的斜率为
所在直线的斜率为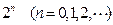 .
.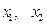
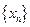 的通项公式
的通项公式
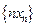 的前
的前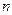 项和为
项和为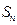 ,求
,求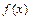 在其定义域上满足
在其定义域上满足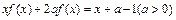 .
.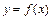 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明);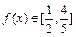 时,求x的取值范围;
时,求x的取值范围;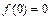 ,数列
,数列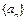 满足
满足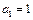 ,那么:
,那么: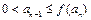 ,正整数N满足
,正整数N满足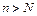 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列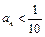 恒成立,求最小的N;
恒成立,求最小的N;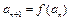 ,求证:
,求证: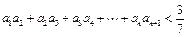 .
.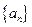 首项
首项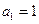 ,前
,前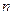 项和
项和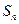 与
与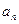 之间满足
之间满足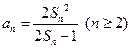 .
.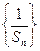 是等差数列;
是等差数列;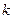 ,使
,使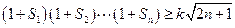 对
对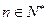 都成立,求
都成立,求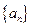 中,
中, ,
,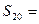
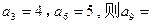
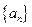 满足
满足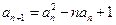 ,
,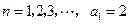 ,通过求
,通过求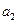 ,
,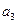 猜想
猜想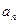 的一个通项公式为( )
的一个通项公式为( )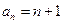
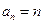
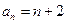
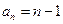
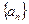 的前3项和
的前3项和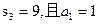 ,则
,则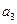 等于
等于