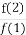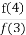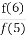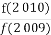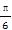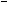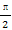Question

“a>3”是“函数f(x)=ax+3在[-1,2]上存在零点”的(　　)

(A)充分而不必要条件 (B)必要而不充分条件

(C)充要条件 (D)既不充分也不必要条件

 

Answer 1

A

【解析】函数f(x)=ax+3在开区间(-1,2)上存在零点的充要条件是f(-1)f(2)=(-a+3)(2a+3)<0,即a>3或a<-;在区间端点处如果f(-1)=0,则a=3,如果f(2)=0,则a=-.因此函数f(x)=ax+3在闭区间[-1,2]上存在零点的充要条件是a≥3或a≤-.根据集合判断充要条件的方法可知,“a>3”是“函数f(x)=ax+3在[-1,2]上存在零点”的充分而不必要条件.