题目内容
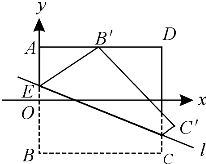 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕,正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B′;折痕l与AB交于点E,点M满足关系式
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕,正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B′;折痕l与AB交于点E,点M满足关系式| EM |
| EB |
| EB′ |
(1)如图,建立以AB中点为原点的直角坐标系,求点M的轨迹方程;
(2)若曲线C是由点M的轨迹及其关于边AB对称的曲线组成的,
F是AB边上的一点,
| BA |
| BF |
| PF |
| FQ |
分析:(1)用消参法求点M的轨迹方程,再所建的直角坐标系中,设M点坐标为(x,y),B′点坐标为(t,1),根据
=
+
,把M点坐标用含参数t的式子表示,再消去参数t,就可得到点M的轨迹方程.
(2)先根据点M的轨迹求其关于边AB对称的曲线方程,可得到曲线C的方程,,再由
=4,过点F的直线交曲线C于P、Q两点,且
=λ
,把λ用直线PQ的斜率k表示,再根据k的范围求λ的范围即可.
| EM |
| EB |
| EB′ |
(2)先根据点M的轨迹求其关于边AB对称的曲线方程,可得到曲线C的方程,,再由
| BA |
| BF |
| PF |
| FQ |
解答: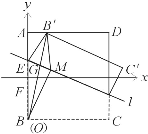 解:(1)以B为原点,BA所在直线为y轴,BC所在直线为x轴,
解:(1)以B为原点,BA所在直线为y轴,BC所在直线为x轴,
建立直角坐标系如图所示:
设B′(t,1),E(0,m),B(0,-1),
其中0≤t≤2,-1≤m≤1.
∴
=
+
,且|
|=|
|,∴BEB′M是菱形,设M(x,y),
则
=(x,y-m),
=(t,2),且
⊥
,即
•
=0
由
•
=0⇒tx+2(y-m)=0
由
=
+
⇒
消去参数t,m,得y=-
x2(0≤x≤2)
(2)依题意知曲线C的方程为:x2=-4y (-2≤x≤2),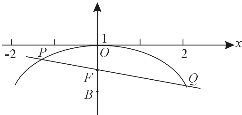
如图设直线PQ的方程为y=kx-
(-
≤k≤
).
代入曲线C的方程并整理,得x2+4kx-2=0.(-2≤x≤2),
设P(x1,y1),Q(x2,y2),则
(*)
又∵
=λ
,,∴(-x1,-
-y1)=λ(x2,y2-
),
从而得x1=-λx2.
代入(*)得
1两边平方除以②式,得
=
,
即
=8k2,∵0≤k2≤(
)2,∴
≤
.
即2λ2-5λ+2≤0,∴
≤λ≤2.∴实数λ的取值范围为[
,2].
 解:(1)以B为原点,BA所在直线为y轴,BC所在直线为x轴,
解:(1)以B为原点,BA所在直线为y轴,BC所在直线为x轴,建立直角坐标系如图所示:
设B′(t,1),E(0,m),B(0,-1),
其中0≤t≤2,-1≤m≤1.
∴
| EM |
| EB |
| EB′ |
| EB′ |
| EB |
则
| EM |
| BB′ |
| EM |
| BB′ |
| EM |
| BB′ |
由
| EM |
| BB′ |
由
| EM |
| EB |
| EB′ |
|
| 1 |
| 4 |
(2)依题意知曲线C的方程为:x2=-4y (-2≤x≤2),

如图设直线PQ的方程为y=kx-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
代入曲线C的方程并整理,得x2+4kx-2=0.(-2≤x≤2),
设P(x1,y1),Q(x2,y2),则
|
又∵
| PF |
| FQ |
| 1 |
| 2 |
| 1 |
| 2 |
从而得x1=-λx2.
代入(*)得
|
1两边平方除以②式,得
| (1-λ)2 |
| -λ |
| (-4k)2 |
| -2 |
即
| (1-λ)2 |
| λ |
| 1 |
| 4 |
| (1-λ)2 |
| λ |
| 1 |
| 2 |
即2λ2-5λ+2≤0,∴
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了消参法求轨迹方程,以及直线与圆锥曲线位置关系的判断.

练习册系列答案
相关题目
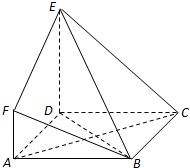 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD.
如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD. 如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为
如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为 (2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.
(2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF. 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):