题目内容
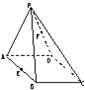 如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD.
如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD.(1)求cos<
| AB |
| PD |
(2)若E为AB的中点,F为PD的中点,求|
| EF |
(3)求二面角P-BC-D的大小.
分析:选取AD中点O为原点,OB、AD、OP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则A(0,-
,0),B(
a,0,0),P(0,0,
a),D(0,
,0).这种解法的好处就是:(1)解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.(2)即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
(1)所以
=(
a,
,0),
=(0,
,-
a),则cos<
,
>=
.
(2)因为E、F分别为AB、PD的中点,所以E(
a,-
,0),F(0,
,
a).则|
|=
a.
(3)因为面PAD⊥面ABCD,PO⊥AD,所以PO⊥面ABCD.因为BO⊥AD,AD∥BC,所以BO⊥BC.连接PB,则PB⊥BC,所以∠PBO为二面角P-BC-D的平面角.
| a |
| 2 |
| ||
| 2 |
| ||
| 2 |
| a |
| 2 |
(1)所以
| AB |
| ||
| 2 |
| a |
| 2 |
| PD |
| a |
| 2 |
| ||
| 2 |
| AB |
| PD |
| 1 |
| 4 |
(2)因为E、F分别为AB、PD的中点,所以E(
| ||
| 4 |
| a |
| 4 |
| a |
| 4 |
| ||
| 4 |
| EF |
| ||
| 4 |
(3)因为面PAD⊥面ABCD,PO⊥AD,所以PO⊥面ABCD.因为BO⊥AD,AD∥BC,所以BO⊥BC.连接PB,则PB⊥BC,所以∠PBO为二面角P-BC-D的平面角.
解答:解:(1)选取AD中点O为原点,OB、AD、OP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则A(0,-
,0),B(
a,0,0),P(0,0,
a),D(0,
,0).
∴
=(
a,
,0),
=(0,
,-
a),
则cos<
,
>=
=
=
.
(2)∵E、F分别为AB、PD的中点,
∴E(
a,-
,0),F(0,
,
a).
则|
|=
=
a.
(3)∵面PAD⊥面ABCD,PO⊥AD,
∴PO⊥面ABCD.
∵BO⊥AD,AD∥BC,∴BO⊥BC.
连接PB,则PB⊥BC,
∴∠PBO为二面角P-BC-D的平面角.
在Rt△PBO中,PO=
a,BO=
a,
∴tan∠PBO=
=
=1.则∠PBO=45°.
故二面角P-BC-D的大小为45°.
| a |
| 2 |
| ||
| 2 |
| ||
| 2 |
| a |
| 2 |
∴
| AB |
| ||
| 2 |
| a |
| 2 |
| PD |
| a |
| 2 |
| ||
| 2 |
则cos<
| AB |
| PD |
| ||||
|
|
| ||||||||||||||||
|
| 1 |
| 4 |
(2)∵E、F分别为AB、PD的中点,
∴E(
| ||
| 4 |
| a |
| 4 |
| a |
| 4 |
| ||
| 4 |
则|
| EF |
(
|
| ||
| 4 |
(3)∵面PAD⊥面ABCD,PO⊥AD,
∴PO⊥面ABCD.
∵BO⊥AD,AD∥BC,∴BO⊥BC.
连接PB,则PB⊥BC,
∴∠PBO为二面角P-BC-D的平面角.
在Rt△PBO中,PO=
| ||
| 2 |
| ||
| 2 |
∴tan∠PBO=
| PO |
| BO |
| ||||
|
故二面角P-BC-D的大小为45°.
点评:本小题主要考查棱锥的结构特征,二面角和线面关系等基本知识,同时考查空间想象能力和推理、运算能力.

练习册系列答案
相关题目
 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为
如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为 (2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.
(2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF. 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):