题目内容
 (2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.
(2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求点F到平面BDE的距离.
分析:(Ⅰ)因为DE⊥平面ABCD,所以DE⊥BD.再由ABCD是正方形,能够证明AC⊥平面BDE.
(Ⅱ)取BE的中点G,设正方形ABCD对角线交于O,所以OG∥DE,OG=
DE,由此入手能够求出F到平面BDE的距离.
(Ⅱ)取BE的中点G,设正方形ABCD对角线交于O,所以OG∥DE,OG=
| 1 |
| 2 |
解答: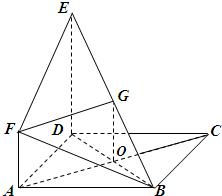 (Ⅰ)证明:因为DE⊥平面ABCD,BD?平面ABCD,
(Ⅰ)证明:因为DE⊥平面ABCD,BD?平面ABCD,
所以DE⊥BD.
又ABCD是正方形,所以AC⊥BD,
而BD∩DE=D,
所以AC⊥平面BDE.
(Ⅱ)解:取BE的中点G,
设正方形ABCD对角线交于O,
所以OG∥DE,OG=
DE,
∵AF∥DE,DE=2AF,
∴AFGO是平行四边形,即FG∥AO,
由(Ⅰ)知AC⊥平面BDE,∴FG⊥平面BDE,
即FG为F到平面BDE的距离,
∵FG=AO=
,
∴F到平面BDE的距离为
.
 (Ⅰ)证明:因为DE⊥平面ABCD,BD?平面ABCD,
(Ⅰ)证明:因为DE⊥平面ABCD,BD?平面ABCD,所以DE⊥BD.
又ABCD是正方形,所以AC⊥BD,
而BD∩DE=D,
所以AC⊥平面BDE.
(Ⅱ)解:取BE的中点G,
设正方形ABCD对角线交于O,
所以OG∥DE,OG=
| 1 |
| 2 |
∵AF∥DE,DE=2AF,
∴AFGO是平行四边形,即FG∥AO,
由(Ⅰ)知AC⊥平面BDE,∴FG⊥平面BDE,
即FG为F到平面BDE的距离,
∵FG=AO=
| 2 |
∴F到平面BDE的距离为
| 2 |
点评:本题考查直线与平面垂直的证明,考查点到平面的距离的求法,解题时要认真审题,仔细解答,注意合理地化立体问题为平面问题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目