题目内容
【题目】如图，底面ABCD是边长为2的菱形，
，
平面ABCD，
，
，BE与平面ABCD所成的角为
.
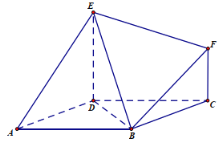
（1）求证：平面
平面BDE；
（2）求二面角B-EF-D的余弦值.
【答案】（1）证明见解析；（2）
【解析】
（1）要证明平面
平面BDE，只需在平面
内找一条直线垂直平面BDE即可；
（2）以O为坐标原点，OA，OB，OG所在直线分别为x、y、z轴建立如图空间直角坐标系，分别求出平面BEF的法向量
，平面
的法向量
，算出
即可.
（1）∵
平面ABCD，
平面ABCD.
∴
.
又∵底面ABCD是菱形，∴
.
∵
，∴
平面BDE，
设AC，BD交于O，取BE的中点G，连FG，OG，
，
，四边形OCFG是平行四边形
，平面BDE
∴
平面BDE，
又因
平面BEF，
∴平面平面BDE.
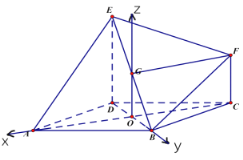
（2）以O为坐标原点，OA，OB，OG所在直线分别为x、y、z轴建立如图空间直角坐标系
∵BE与平面ABCD所成的角为
，
，
，
，
，
，
.
，
设平面BEF的法向量为
，
，
，
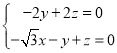设平面的法向量
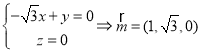
设二面角
的大小为
.
.
练习册系列答案
相关题目
【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛，抽取了近期两人
次数学考试的成绩，统计结果如下表：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩(分) |
|
|
|
|
|
乙的成绩(分) |
|
|
|
|
|
(1)若从甲、乙两人中选出一人参加数学竞赛，你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛，在初赛中有两种答题方案：
方案一：每人从道备选题中任意抽出
道，若答对，则可参加复赛，否则被淘汰.
方案二：每人从道备选题中任意抽出
道，若至少答对其中
道，则可参加复赛，否则被润汰.
已知学生甲、乙都只会道备选题中的道，那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
