Question

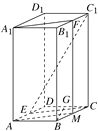
【题目】(2017·泰安模拟)如图，在正四棱柱ABCDA1B1C1D1中，E为AD的中点，F为B1C1的中点．

(1)求证：A1F∥平面ECC1；

(2)在CD上是否存在一点G，使BG⊥平面ECC1？若存在，请确定点G的位置，并证明你的结论，若不存在，请说明理由．

Answer 1

【答案】（1）见解析（2）见解析

【解析】试题分析:(1) 取BC的中点M，易得A1F∥AM, ,CE∥AM，所以CE∥A1F.再根据线面平行判定定理得结论 (2) 作BG⊥EC.则G为CD的中点时,由线面垂直性质得CC1⊥BG.再根据线面垂直判定定理得结论

试题解析:解：(1)证明：如图，在正四棱柱ABCDA1B1C1D1中，取BC的中点M，连接AM，FM，

所以B1F∥BM且B1F＝BM，

所以四边形B1FMB是平行四边形，

所以FM∥B1B且FM＝B1B.

因为B1B∥A1A且B1B＝A1A，

所以FM∥A1A且FM＝A1A，

所以四边形AA1FM是平行四边形，所以A1F∥AM.

因为E为AD的中点，

所以AE∥MC且AE＝MC.

所以四边形AMCE是平行四边形，

所以CE∥AM，所以CE∥A1F.

因为A1F平面ECC1，EC平面ECC1，

所以A1F∥平面ECC1.

(2)在CD上存在一点G，使BG⊥平面ECC1.

证明如下：取CD的中点G，连接BG.

在正方形ABCD中，DE＝GC，CD＝BC，∠ADC＝∠BCD，

所以△CDE≌△BCG，

所以∠ECD＝∠GBC.

因为∠CGB＋∠GBC＝90°，

所以∠CGB＋∠DCE＝90°，所以BG⊥EC.

因为CC1⊥平面ABCD，BG平面ABCD，

所以CC1⊥BG.又EC∩CC1＝C，

所以BG⊥平面ECC1.

故当G为CD的中点时，满足BG⊥平面ECC1.