题目内容
【题目】某工厂为了对研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
附：对于一组数据
，其回归直线
的斜率的最小二乘估计值为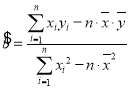
；
本题参考数值：
.
（1）若销量y与单价x服从线性相关关系，求该回归方程；
（2）在（1）的前提下，若该产品的成本是5元/件，问：产品该如何确定单价，可使工厂获得最大利润.
【答案】（1）
（2）该产品的单价应定为9.5元
【解析】
(1)先求
，再代入公式求得
，则方程可解
（2）列出利润
的函数关系，利用二次函数求最值即可
（1）∵
又
所以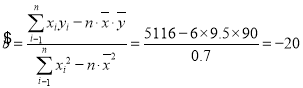
故回归方程为.
（2）设该产品的售价为x元，工厂利润为L元，当
时，利润
，定价不合理.
由
得
，故
，当
时，
取得最大值.
因此，为使工厂获得最大利润，该产品的单价应定为9.5元
【题目】某次文艺汇演为，要将A，B，C，D，E，F这六个不同节目编排成节目单，如下表：
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
节目 |
如果A，B两个节目要相邻，且都不排在第3号位置，那么节目单上不同的排序方式有
A. 192种B. 144种C. 96种D. 72种
【题目】为考察某种药物预防疾病的效果，进行动物试验，调查了 105 个样本，统计结果为：服药的共有 55 个样本，服药但患病的仍有 10 个样本，没有服药且未患病的有 30个样本.
（1）根据所给样本数据完成 
列联表中的数据；
（2）请问能有多大把握认为药物有效？
(参考公式：
独立性检验临界值表
概率 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
患病 | 不患病 | 合计 | |
服药 | |||
没服药 | |||
合计 |
【题目】为了调查某校高二学生的身高是否与性别有关，随机调查该校64名高二学生，得到2×2列联表如表：
男生 | 女生 | 总计 | |
身高低于170cm | 8 | 24 | 32 |
身高不低于170cm | 26 | 6 | 32 |
总计 | 34 | 30 | 64 |
附：K2
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
由此得出的正确结论是（ ）
A.在犯错误的概率不超过0.01的前提下，认为“身高与性别无关”
B.在犯错误的概率不超过0.01的前提下，认为“身高与性别有关”
C.有99.9%的把握认为“身高与性别无关”
D.有99.9%的把握认为“身高与性别有关”
