题目内容
下列判断正确的是( )
A.“ ”是“ ”是“ ”的充要条件 ”的充要条件 |
B.命题“ ”的否定是“ ”的否定是“ ” ” |
C.若 均为假命题,则 均为假命题,则 为真命题 为真命题 |
| D.一个命题连同它的逆命题、否命题、逆否命题,这四个命题中不可能恰有一个真命题 |
D
解析试题分析:显然,“ ”
”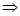 “
“ ”,但取
”,但取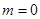 ,则“
,则“ ”
”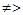 “
“ ”,所以“
”,所以“ ”是“
”是“ ”的充分步必要条件,故A项错误;命题
”的充分步必要条件,故A项错误;命题
“ ”的否定是“
”的否定是“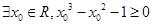 ”,故B项错误;由于命题q为假命题,则
”,故B项错误;由于命题q为假命题,则 也为假命题,故C项错误;一个命题连同它的逆命题、否命题、逆否命题,这四个命题可分成两组逆否命题,由于互为逆否命题得两个命题真假性一致,故这四个命题中不可能恰有一个真命题,D项正确。所以选D。
也为假命题,故C项错误;一个命题连同它的逆命题、否命题、逆否命题,这四个命题可分成两组逆否命题,由于互为逆否命题得两个命题真假性一致,故这四个命题中不可能恰有一个真命题,D项正确。所以选D。
考点:命题的真假性
点评:判断命题的真假性是一个考点,这种题目涉及知识点多,因而比较难,所以可用到排除法。

练习册系列答案
相关题目
对于指数函数 则
则 ,是“
,是“ 是
是 上的单调函数”的
上的单调函数”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设a,b为实数,则“0<ab<l”是“ ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若函数f(x)和g(x)的定义域、值域都是R,则不等式f(x)> g(x)有解的充要条件是( )
| A.$ x∈R, f(x)>g(x) | B.有无穷多个x (x∈R ),使得f(x)>g(x) |
| C." x∈R,f(x)>g(x) | D.{ x∈R| f(x)≤g(x)}=F |
设p:log2x<0,q: x-1>1,则p是q的 ( ).
x-1>1,则p是q的 ( ).
| A.充要条件 | B.充分不必要条件 | C.必要不充分条件 | D.既不充分也不必要条件 |
“a=-3”是“函数f(x)=|x-a|在区间[-3,+∞)上为增函数”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“对任意的 ”的否定是
”的否定是
A.不存在 | B.存在 |
C.存在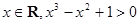 | D.对任意的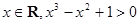 |
已知条件 :
: ,条件
,条件 :
: ,则
,则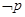 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
已知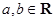 ,下列四个条件中,使“
,下列四个条件中,使“ ”成立的必要而不充分的条件是( )
”成立的必要而不充分的条件是( )
A. | B. | C. | D. |