题目内容
【题目】三棱锥P﹣ABC，底面ABC为边长为2 
的正三角形，平面PBC⊥平面ABC，PB=PC=2，D为AP上一点，AD=2DP，O为底面三角形中心． 
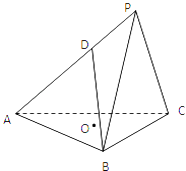
（1）求证DO∥面PBC；
（2）求证：BD⊥AC；
（3）设M为PC中点，求平面MBD和平面BDO所成锐二面角的余弦值．
【答案】
（1）证明：连接AO交BC于点E，连接PE．
∵O为正三角形ABC的中心，∴AO=2OE，
且E为BC中点．又AD=2DP，
∴DO∥PE，
∵DO平面PBC，PE平面PBC
∴DO∥面PBC．
（2）证明：∵PB=PC，且E为BC中点，∴PE⊥BC，
又平面PBC⊥平面ABC，
∴PE⊥平面ABC，
由（Ⅰ）知，DO∥PE，
∴DO⊥平面ABC，
∴DO⊥AC
连接BO，则AC⊥BO，又DO∩BO=O，
∴AC⊥平面DOB，∴AC⊥BD．
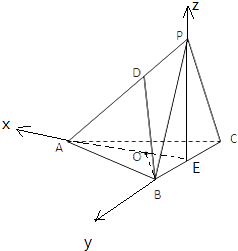
（3）解：由（1）（2）知，EA，EB，EP两两互相垂直，且E为BC中点，
所以分别以EA，EB，EP所在直线为x，y，z轴，建立空间直角坐标系，
如图，则A（3，0，0），B（0， 
，0），P（0，0，1），
D（1，0， 
），C（0，﹣ ，0），M（0，﹣ 
， 
），
∴ 
=（0，﹣ 
， ）， 
=（﹣1， ，﹣ ），
设平面BDM的法向量为 
=（x，y，z），则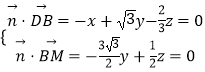 
，
令y=1，则 =（﹣ ，1，3 ），
由（Ⅱ）知AC⊥平面DBO，
∴ 
=（﹣3，﹣ ，0）为平面DBO的法向量，
∴cos＜ 
＞= 
= 
= 
，
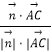由图可知，二面角M﹣BD﹣O的余弦值为 ．
【解析】（1）连接AO交BC于点E，连接PE，推导出DO∥PE，由此能证明DO∥面PBC．（2）推导出PE⊥BC，从而PE⊥平面ABC，进而DO⊥平面ABC，由此得DO⊥AC，再由AC⊥BO，能证明AC⊥BD．（3）分别以EA，EB，EP所在直线为x，y，z轴，建立空间直角坐标系，利用向量法能求出二面角M﹣BD﹣O的余弦值．
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识，掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点，以及对直线与平面平行的判定的理解，了解平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
