题目内容
已知函数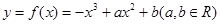
(1)若函数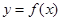 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;
(2)设函数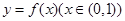 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求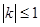 的充要条件;
的充要条件;
(3)若函数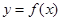 的图象上任意不同的两点的连线的斜率小于l,求证
的图象上任意不同的两点的连线的斜率小于l,求证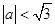 .
.
(1)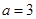 ,
,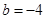 ;(2)
;(2)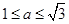 ;(3)
;(3)
解析试题分析:(1)由函数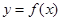 的图象切x轴于点(2,0),得
的图象切x轴于点(2,0),得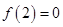 且
且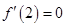 ,解方程组可得
,解方程组可得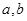 的值.
的值.
(2)由于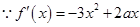 ,根据导数的几何意义,任意不同的两点的连线的斜率小于l,
,根据导数的几何意义,任意不同的两点的连线的斜率小于l,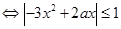 对任意的
对任意的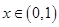 恒成立,利用分离变量法,转化为
恒成立,利用分离变量法,转化为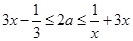 对任意的
对任意的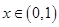 恒成立,进一步转化为函数的最值问题;
恒成立,进一步转化为函数的最值问题;
(3)设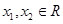 ,则
,则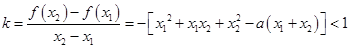
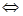
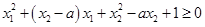 对
对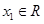 恒成立
恒成立
将上不等式看成是关于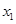 的一元二次不等式即可.
的一元二次不等式即可.
解:(1)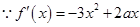
由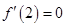 ,得
,得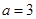 ,
,
又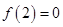 ,得
,得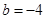
(2)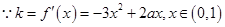
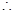 对任意的
对任意的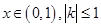 ,即
,即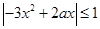 对任意的
对任意的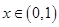 恒成立
恒成立
等价于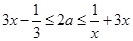 对任意的
对任意的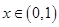 恒成立
恒成立
令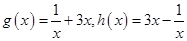
则
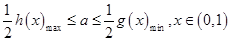
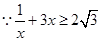 ,当且仅当
,当且仅当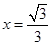 时“=”成立,
时“=”成立,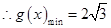
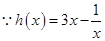 在
在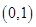 上为增函数,
上为增函数,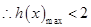
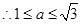
(3)设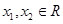 ,则
,则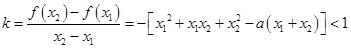
即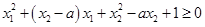 ,对
,对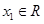 恒成立
恒成立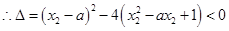 ,对
,对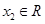 恒成立
恒成立
即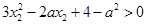 ,对
,对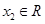 恒成立
恒成立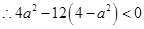
解得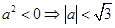
考点:1、导数的几何意义;2、等价转化的思想;3、二次函数与一元二次一不等式问题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
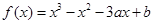 .
.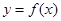 在点
在点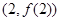 处与直线
处与直线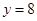 相切,求a,b的值;
相切,求a,b的值; 的单调区间.
的单调区间.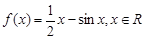 .
. 的递减区间;
的递减区间;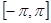 上的最值.
上的最值. ,曲线
,曲线 经过点
经过点 ,
, 处的切线为
处的切线为 .
. 、
、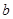 的值;
的值; ,使得
,使得 时,
时, 恒成立,求
恒成立,求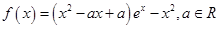 .
.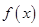 在
在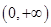 内单调递增,求
内单调递增,求 的取值范围;
的取值范围;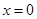 处取得极小值,求
处取得极小值,求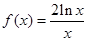
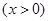
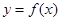 在
在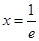 处的切线的斜率;
处的切线的斜率;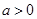 ,求函数
,求函数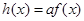 在
在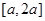 上的最大值.
上的最大值. 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)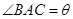 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为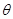 的函数
的函数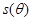 ;
;
 ,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
 ,求曲线
,求曲线 在
在 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.