题目内容
已知函数f(x)=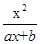 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)<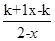 .
.
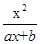 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)<
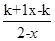 .
.(1)f(x)= (x≠2)
(x≠2)
(2)当1<k<2时,原不等式的解集为{x|1<x<k或x>2};
当k=2时,原不等式的解集为{x|x>1且x≠2};
当k>2时,原不等式的解集为{x|1<x<2或x>k}.
 (x≠2)
(x≠2)(2)当1<k<2时,原不等式的解集为{x|1<x<k或x>2};
当k=2时,原不等式的解集为{x|x>1且x≠2};
当k>2时,原不等式的解集为{x|1<x<2或x>k}.
试题分析:解: (1)将x1=3,x2=4分别代入方程
 -x+12=0,得
-x+12=0,得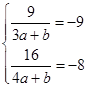 , 3分
, 3分解得
 .
.∴f(x)=
 (x≠2) 5分
(x≠2) 5分(2)原不等式即为
 <
< ,可化为
,可化为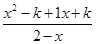 <0. 6分
<0. 6分即(x-2)(x-1)(x-k)>0. 7分
①当1<k<2时,1<x<k或x>2; 9分
②当k=2时,x>1且x≠2; 10分
③当k>2时,1<x<2或x>k. 12分
综上所述,当1<k<2时,原不等式的解集为{x|1<x<k或x>2};
当k=2时,原不等式的解集为{x|x>1且x≠2};
当k>2时,原不等式的解集为{x|1<x<2或x>k}. 13分
点评:主要是考查了函数解析式以及一元二次不等式的求解,体现了分类讨论思想的运用,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
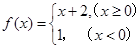 ,则
,则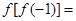 ( )
( )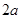 人,(
人,(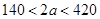 ,且
,且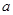 为偶数),每人每年可创利
为偶数),每人每年可创利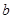 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利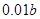 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年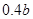 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?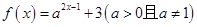 恒过定点________ ____.
恒过定点________ ____.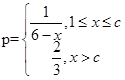 (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.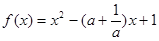 ,
,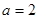 时,解不等式
时,解不等式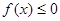 ;
;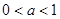 ,解关于
,解关于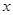 的不等式
的不等式 为全集,
为全集, ,则
,则 ( )
( )



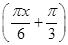 (0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.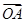 ·
·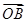 的值;
的值;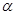 、
、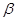 的终边上,求tan(
的终边上,求tan(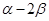 )的值.
)的值.