题目内容
已知双曲线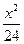 -
-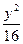 =1,P为双曲线上一点,F1、F2是双曲线的两个焦点,并且∠F1PF2=60°,求△F1PF2的面积.
=1,P为双曲线上一点,F1、F2是双曲线的两个焦点,并且∠F1PF2=60°,求△F1PF2的面积.
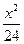 -
-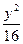 =1,P为双曲线上一点,F1、F2是双曲线的两个焦点,并且∠F1PF2=60°,求△F1PF2的面积.
=1,P为双曲线上一点,F1、F2是双曲线的两个焦点,并且∠F1PF2=60°,求△F1PF2的面积.16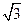 ..
..
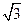 ..
..|F1F2|2=4c2=4×(24+16)=160.在△F1PF2中,由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|
cos60°.
∴|PF1|2+|PF2|2-|PF1||PF2|="160. " ①
又∵|PF1|-|PF2|=±2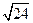 ,
,
∴|PF1|2-2|PF1||PF2|+|PF2|2="96. " ②
①-②,得|PF1|·|PF2|=64.
∴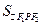 =
=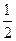 |PF1||PF2|sin60°=
|PF1||PF2|sin60°=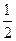 ×64×
×64×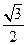 =16
=16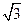 .
.
cos60°.
∴|PF1|2+|PF2|2-|PF1||PF2|="160. " ①
又∵|PF1|-|PF2|=±2
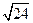 ,
,∴|PF1|2-2|PF1||PF2|+|PF2|2="96. " ②
①-②,得|PF1|·|PF2|=64.
∴
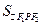 =
=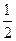 |PF1||PF2|sin60°=
|PF1||PF2|sin60°=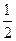 ×64×
×64×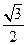 =16
=16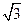 .
.
练习册系列答案
相关题目

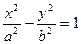 (a>0,b>0)的右准线
(a>0,b>0)的右准线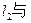 一条渐近线
一条渐近线 交于两点P、Q,F是双曲线的右焦点。
交于两点P、Q,F是双曲线的右焦点。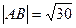 ,求双曲线的方程;
,求双曲线的方程; 和左支分别为点M、N,若M为PN的中点,求双曲线的离心率e。
和左支分别为点M、N,若M为PN的中点,求双曲线的离心率e。 的中心在原点,对称轴为坐标轴,其一条渐近线方程是
的中心在原点,对称轴为坐标轴,其一条渐近线方程是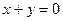 ,且双曲线
,且双曲线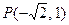 .
.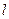 过点
过点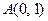 ,其方向向量为
,其方向向量为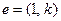
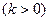 ,令向量
,令向量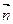 满足
满足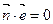 .双曲线
.双曲线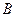 ,使得
,使得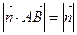 . 若存在,求出对应的
. 若存在,求出对应的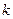 值和
值和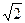 )、(
)、(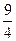 ,5),则双曲线的标准方程为( )
,5),则双曲线的标准方程为( ) ="1"
="1"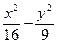 ="1"
="1"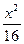 -
-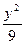 =1上的一点P到点(5,0)的距离为15,则点P到点(-5,0)的距离是( )
=1上的一点P到点(5,0)的距离为15,则点P到点(-5,0)的距离是( )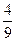 ,求双曲线的方程.
,求双曲线的方程.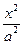 -
-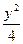 =1过点(-3
=1过点(-3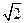 ,2),则该双曲线的焦距为__________.
,2),则该双曲线的焦距为__________. ,并且与直线y=
,并且与直线y=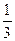 (x-4)相交所得线段的中点的横坐标为-
(x-4)相交所得线段的中点的横坐标为-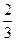 ,求这个双曲线的方程.
,求这个双曲线的方程.