题目内容
已知双曲线
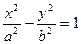 (a>0,b>0)的右准线
(a>0,b>0)的右准线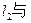 一条渐近线
一条渐近线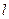 交于两点P、Q,F是双曲线的右焦点。
交于两点P、Q,F是双曲线的右焦点。
(I)求证:PF⊥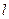 ;
;
(II)若△PQF为等边三角形,且直线y=x+b交双曲线于A,B两点,且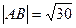 ,求双曲线的方程;
,求双曲线的方程;
(III)延长FP交双曲线左准线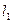 和左支分别为点M、N,若M为PN的中点,求双曲线的离心率e。
和左支分别为点M、N,若M为PN的中点,求双曲线的离心率e。

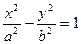 (a>0,b>0)的右准线
(a>0,b>0)的右准线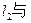 一条渐近线
一条渐近线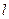 交于两点P、Q,F是双曲线的右焦点。
交于两点P、Q,F是双曲线的右焦点。(I)求证:PF⊥
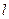 ;
;(II)若△PQF为等边三角形,且直线y=x+b交双曲线于A,B两点,且
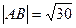 ,求双曲线的方程;
,求双曲线的方程;(III)延长FP交双曲线左准线
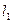 和左支分别为点M、N,若M为PN的中点,求双曲线的离心率e。
和左支分别为点M、N,若M为PN的中点,求双曲线的离心率e。(1) 证明见解析
(2)双曲线方程为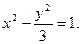
(3)e=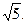
(2)双曲线方程为
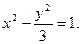
(3)e=
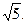
(1) 不妨设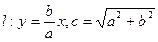 .
.
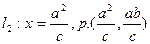 , F.(c,0)
, F.(c,0)
设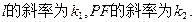
k2=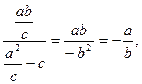 ∴k1k2=-1.
∴k1k2=-1.
即PF⊥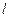 .
.
(2)由题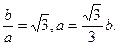
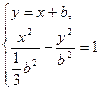 . x2-bx-b2="0,"
. x2-bx-b2="0," 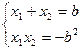
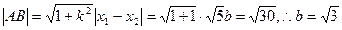
∴a="1," ∴双曲线方程为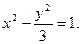
(3)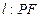 y=-
y=-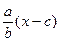 M(-
M(-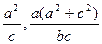
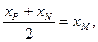 ∴N(-
∴N(-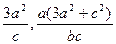 ).
).
又N在双曲线上。∴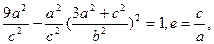
∴e=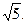
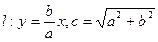 .
.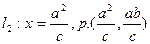 , F.(c,0)
, F.(c,0)设
k2=
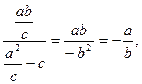 ∴k1k2=-1.
∴k1k2=-1.即PF⊥
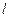 .
. (2)由题
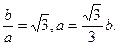
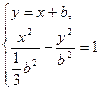 . x2-bx-b2="0,"
. x2-bx-b2="0," 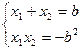
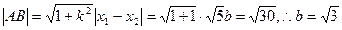
∴a="1," ∴双曲线方程为
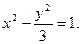
(3)
 y=-
y=-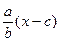 M(-
M(-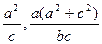
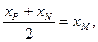 ∴N(-
∴N(-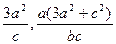 ).
).又N在双曲线上。∴
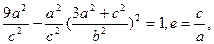
∴e=

练习册系列答案
相关题目
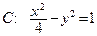 ,
,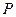 为
为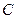 上的任意点。
上的任意点。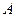 的坐标为
的坐标为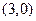 ,求
,求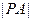 的最小值.
的最小值.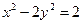 的左、右两个焦点为
的左、右两个焦点为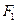 ,
, 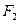 ,动点P满
,动点P满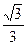 ,
,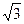 ],求实数m的取值范围;
],求实数m的取值范围;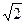 +1时,△APQ的内心恰好是点M,求此双曲线的方程.
+1时,△APQ的内心恰好是点M,求此双曲线的方程.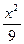 -
-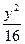 =1的两个焦点为F1、F2,点P在双曲线上,若PF1⊥PF2,则点P到x轴的距离为__________________.
=1的两个焦点为F1、F2,点P在双曲线上,若PF1⊥PF2,则点P到x轴的距离为__________________.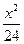 -
-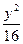 =1,P为双曲线上一点,F1、F2是双曲线的两个焦点,并且∠F1PF2=60°,求△F1PF2的面积.
=1,P为双曲线上一点,F1、F2是双曲线的两个焦点,并且∠F1PF2=60°,求△F1PF2的面积.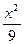 -
-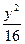 =1只有一个公共点的直线共有______________条.
=1只有一个公共点的直线共有______________条.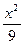 -
-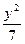 ="1(x>0)"
="1(x>0)"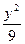 -
-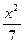 ="1(y>0)"
="1(y>0)"