题目内容
设函数f(x)=x2-x+b,且f(log2a)=b,log2[f(a)]=2(a≠1),求f(log2x)的最小值及对应的x的值.
由已知得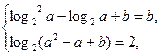
即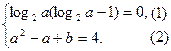
由①得log2a=1,∴a=2.
代入②得b=2.∴f(x)=x2-x+2.
∴f(log2x)=log22x-log2x+2=(log2x-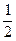 )2+
)2+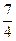 .∴当log2x=
.∴当log2x=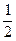 时,f(log2x)取得最小值
时,f(log2x)取得最小值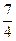 ,此时x=
,此时x=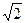 .
.
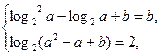
即
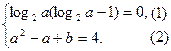
由①得log2a=1,∴a=2.
代入②得b=2.∴f(x)=x2-x+2.
∴f(log2x)=log22x-log2x+2=(log2x-
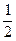 )2+
)2+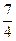 .∴当log2x=
.∴当log2x=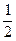 时,f(log2x)取得最小值
时,f(log2x)取得最小值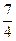 ,此时x=
,此时x=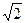 .
.关键是利用已知的两个条件求出a、b的值.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
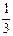 (结果保留1个有效数字)?(
(结果保留1个有效数字)?(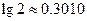 ,
,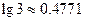 )
)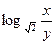 的值
的值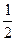 )
)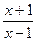 +log2(x-1)+log2(p-x)的值域.
+log2(x-1)+log2(p-x)的值域.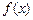 是定义域为R的奇函数,若当
是定义域为R的奇函数,若当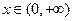 时,
时,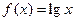 ,则满足
,则满足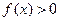 的
的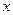 的取值范围是 .
的取值范围是 .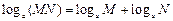
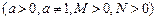 .已知
.已知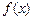 、
、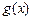 互为反函数
互为反函数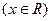 ,若函数
,若函数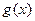 有性质:对于任意的实数
有性质:对于任意的实数 ,有
,有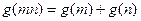 ,通过类比的思想,猜想函数
,通过类比的思想,猜想函数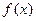 性质:___________________________________________.
性质:___________________________________________.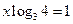 ,求
,求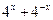 的值.
的值.