题目内容
设函数y=f(x),且lg(lgy)=lg3x+lg(3-x).
(1)求f(x)的表达式及定义域；
（2）求f(x)的值域.
(1)求f(x)的表达式及定义域；
（2）求f(x)的值域.
（1）定义域为（0，3）.
(2) y=f(x)的值域为（1，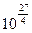
］.
(2) y=f(x)的值域为（1，
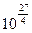］.（1）∵lg(lgy)=lg(3x)+lg(3-x),
∴
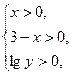即
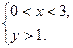
又∵lg(lgy)=lg(3x)+lg(3-x),
∴lg(lgy)=lg［3x(3-x)］,lgy=3x(3-x),
∴y=103x(3-x),其中0<x<3,即定义域为（0，3）.
(2)令u=3x(3-x),
则u=-3(x-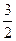
)2+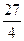
(0<x<3),∴0<-3x2+9x≤,
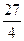∴1<y≤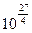.∴y=f(x)的值域为（1，］.
∴
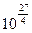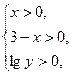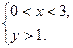
即又∵lg(lgy)=lg(3x)+lg(3-x),
∴lg(lgy)=lg［3x(3-x)］,lgy=3x(3-x),
∴y=103x(3-x),其中0<x<3,即定义域为（0，3）.
(2)令u=3x(3-x),
则u=-3(x-
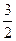)2+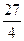(0<x<3),∴0<-3x2+9x≤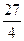,∴1<y≤
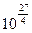.∴y=f(x)的值域为（1，］.
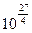练习册系列答案
口算能手系列答案
相关题目
+
=2,则A的值为（ ）
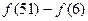的值； （2）若
，求
的取值范围。
的定义域是（ ）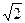
，-1］∪（1,
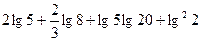的值为 。
，则
的值为（ ）
