题目内容
【题目】设复数![]() 与复平面上点
与复平面上点![]() 对应.
对应.
(1)若![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的一个虚根,且
的一个虚根,且![]() ,求实数
,求实数![]() 的值;
的值;
(2)设复数![]() 满足条件
满足条件![]() (其中
(其中![]() 、常数
、常数![]() ),当
),当![]() 为奇数时,动点
为奇数时,动点![]() 的轨迹为
的轨迹为![]() ,当
,当![]() 为偶数时,动点
为偶数时,动点![]() 的轨迹为
的轨迹为![]() ,且两条曲线都经过点
,且两条曲线都经过点![]() ,求轨迹
,求轨迹![]() 与
与![]() 的方程;
的方程;
(3)在(2)的条件下,轨迹![]() 上存在点
上存在点![]() ,使点
,使点![]() 与点
与点![]() 的最小距离不小于
的最小距离不小于![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)m=4;(2)C1的方程是:![]() (x
(x![]() ),C2的方程是:
),C2的方程是:![]() .(3)
.(3)![]() 或
或![]() .
.
【解析】
(1)由实系数方程虚根成对,利用韦达定理直接求出m的值.
(2)方法一:分n为奇数和偶数,化出a的范围,联立双曲线方程,求出a值,推出双曲线方程即可.
方法二:由题意分a的奇偶数,联立方程组,求出复数β,解出a,根据双曲线的定义求出双曲线方程.
(3)设点A的坐标,求出|AB|表达式,根据x范围,x的对称轴讨论![]() ,
,![]() 时,|AB|的最小值,不小于
时,|AB|的最小值,不小于![]() ,求出实数x0的取值范围.
,求出实数x0的取值范围.
(1)β是方程的一个虚根,则![]() 是方程的另一个虚根,
是方程的另一个虚根,
则![]() ,所以m=4
,所以m=4
(2)方法1:①当n为奇数时,|![]() +3|﹣|
+3|﹣|![]() ﹣3|=2a,常数
﹣3|=2a,常数![]() ),
),
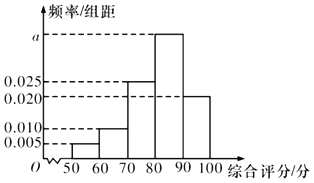
轨迹C1为双曲线一支,其方程为![]() ,x≥a;
,x≥a;
②当n为偶数时,|![]() +3|+|
+3|+|![]() ﹣3|=4a,常数
﹣3|=4a,常数![]() ),
),
轨迹C2为椭圆,其方程为![]() ;
;
依题意得方程组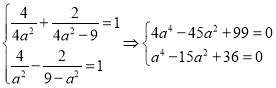
解得a2=3,
因为![]() ,所以
,所以![]() ,
,
此时轨迹为C1与C2的方程分别是:![]() ,x
,x![]() ,
,![]() .
.
方法2:依题意得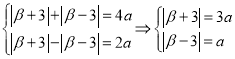
轨迹为C1与C2都经过点![]() ,且点
,且点![]() 对应的复数
对应的复数![]() ,
,
代入上式得![]() ,
,
即![]() 对应的轨迹C1是双曲线,方程为
对应的轨迹C1是双曲线,方程为![]() ;
;
![]() 对应的轨迹C2是椭圆,方程为
对应的轨迹C2是椭圆,方程为![]() .
.
(3)由(2)知,轨迹C2:![]() ,设点A的坐标为(x,y),
,设点A的坐标为(x,y),
则![]()
![]() ,
,![]()
当![]() 即
即![]() 时,
时,![]()
当![]() 即
即![]() 时,
时,![]() ,
,
综上![]() 或
或![]() .
.

练习册系列答案
相关题目