题目内容
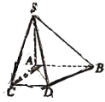
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 是菱形,
是菱形,![]() .
.

(1)证明:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,可证
,可证![]() 平面
平面![]() ,得B1C⊥AO,B10=CO,进而可得AC=AB1;(2)先根据已知条件证明
,得B1C⊥AO,B10=CO,进而可得AC=AB1;(2)先根据已知条件证明![]() 平面
平面![]() 以
以![]() 为原点,
为原点,![]() 所在直线为坐标轴建立空间直角坐标系
所在直线为坐标轴建立空间直角坐标系![]() ,求得平面
,求得平面![]() 的一个法向量,然后利用向量公式即可求得结果.
的一个法向量,然后利用向量公式即可求得结果.
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵四边形![]() 是菱形,∴
是菱形,∴![]() 且
且![]() 为
为![]() 中点,
中点,
∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,∴
,∴![]() ,
,
![]() 为
为![]() 中点,
中点,![]() 为
为![]() 的垂直平分线,
的垂直平分线,
∴![]() .
.
(2)不妨设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,![]()
又![]() ,
,![]() ,∴
,∴![]() 平面
平面![]()
(方法一)以![]() 为原点,
为原点,![]() 所在直线为坐标轴建立空间直角坐标系
所在直线为坐标轴建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
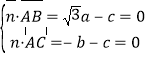 ,
,
![]() ,设
,设![]() ,
,
直线![]() 与平面
与平面![]() 所成角的正弦值,即直线
所成角的正弦值,即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为
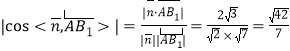
(方法二)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
三棱锥![]() 的体积
的体积![]()
三棱锥![]() 的体积
的体积![]()
解![]() ,得
,得![]()
直线![]() 与平面
与平面![]() 所成角的正弦值,即直线
所成角的正弦值,即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
| π |
| 2π |
x |
|
| |||
| 0 | 4 | -4 | 0 |
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数f(x)的解析式;
(2)将![]() 图象上所有点向左平行移动θ(
图象上所有点向左平行移动θ(![]() )个单位长度,得到
)个单位长度,得到![]() 的图象.若
的图象.若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求θ的最小值.
,求θ的最小值.
【题目】在中学生综合素质评价某个维度的测评中,分优秀、合格、尚待改进三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表一:男生
男生 | 等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 |
| 5 |
表二:女生
女生 | 等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 |
|
(1)求![]() ,
,![]() 的值;
的值;
(2)从表二的非优秀学生中随机抽取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(3)由表中统计数据填写![]() 列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 | 45 |
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.01 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |