题目内容
【题目】已知函数![]() ,
, ![]() 在
在![]() 和
和![]() 处取得极值,且
处取得极值,且![]() ,曲线
,曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)证明关于![]() 的方程
的方程![]() 至多只有两个实数根(其中
至多只有两个实数根(其中![]() 是
是![]() 的导函数,
的导函数, ![]() 是自然对数的底数).
是自然对数的底数).
【答案】(Ⅰ)![]() (Ⅱ)见解析.
(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)先求![]() ,根据韦达定理及
,根据韦达定理及![]() 列出关于
列出关于![]() 的方程组,进而可得结果;(Ⅱ)圆方程等价于
的方程组,进而可得结果;(Ⅱ)圆方程等价于![]() ,令
,令![]() ,研究函数
,研究函数![]() 的单调性,讨论
的单调性,讨论![]() 与
与![]() 两种情况分别证明即可.
两种情况分别证明即可.
试题解析:(Ⅰ) ![]() ,因为
,因为![]() 在
在![]() 和
和![]() 处取得极值,
处取得极值,
所以![]() 和
和![]() 是方程
是方程![]() 的两个根,则
的两个根,则![]() ,
, ![]() ,
,
又![]() ,则
,则![]() ,所以
,所以![]() .
.
由已知曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,所以可得
垂直,所以可得![]() ,
,
即![]() ,由此可得
,由此可得![]() 解得
解得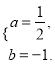
所以![]()
(Ⅱ)对于![]() ,
,
(1)当![]() 时,得
时,得![]() ,方程无实数根;
,方程无实数根;
(2)当![]() 时,得
时,得![]() ,令
,令![]() ,
,
![]()
![]() ,
,
当![]() 时,
时, ![]() ;
;
当![]() 或
或![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
∴![]() 的单调递减区间是
的单调递减区间是![]() 和
和![]() ,单调递增区间是
,单调递增区间是![]() ,
,
函数![]() 在
在![]() 和
和![]() 处分别取得极小值和极大值.
处分别取得极小值和极大值.
![]() ,
, ![]() ,
,
对于![]() ,由于
,由于![]() 恒成立,
恒成立,
且![]() 是与
是与![]() 轴有两个交点、开口向上的抛物线,
轴有两个交点、开口向上的抛物线,
所以曲线![]() 与
与![]() 轴有且只有两个交点,从而
轴有且只有两个交点,从而![]() 无最大值,
无最大值, ![]() .
.
若![]() 时
时![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 至多有两个交点;
至多有两个交点;
若![]()
![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 只有一个交点;
只有一个交点;
综上所述,无论![]() 取何实数,方程
取何实数,方程![]() 至多只有两实数根.
至多只有两实数根.

练习册系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: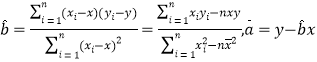 .
.