题目内容
已知数列 的前n项和为
的前n项和为 ,
, =1,且
=1,且
 .
.
(1)求 ,
, 的值,并求数列
的值,并求数列 的通项公式;
的通项公式;
(2)解不等式
 .
.
(1)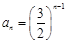 (2)根据数列的规律性,通过放缩法来得到证明。
(2)根据数列的规律性,通过放缩法来得到证明。
解析试题分析:(1)∵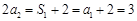 ,∴
,∴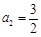 . 1分
. 1分
∵ ,∴
,∴ . 2分
. 2分
∵ ,∴
,∴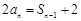 (n≥2),
(n≥2),
两式相减,得 .
.
∴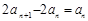 .则
.则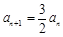 (n≥2). 4分
(n≥2). 4分
∵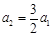 ,∴
,∴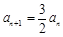
 . 5分
. 5分
∵ ,∴
,∴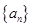 为等比数列,
为等比数列,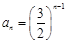 . 7分
. 7分
(2)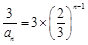 ,
,
∴数列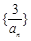 是首项为3,公比为
是首项为3,公比为 等比数列. 8分
等比数列. 8分
数列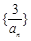 的前5项为:3,2,
的前5项为:3,2,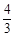 ,
, ,
,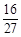 .
.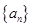 的前5项为:1,
的前5项为:1,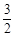 ,
,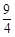 ,
,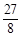 ,
, .
.
∴n=1,2,3时,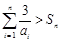 成立; 11分
成立; 11分
而n=4时,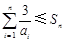 ; 12分
; 12分
∵n≥5时,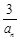 <1,an>1,∴
<1,an>1,∴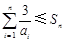 . 14分
. 14分
∴不等式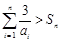
 的解集为{1,2,3}. 16分
的解集为{1,2,3}. 16分
考点:等比数列,以及数列的求和
点评:解决的关键是能熟练的根据等比数列的通项公式来得到表达式,同时能结合不等式的性质来放缩得到证明,属于中档题。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
 }的前n项和为
}的前n项和为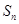 ,
,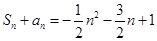 ,
,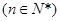 .
. ,证明:数列
,证明:数列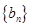 是等比数列;
是等比数列;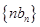 的前
的前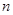 项和
项和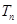 ;
;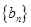 满足
满足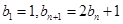 ,若数列
,若数列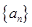 满足:
满足: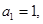 ,且当
,且当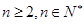 时,
时,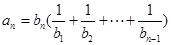
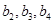 及
及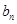 ;
; ,(注:
,(注: ).
).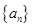 满足
满足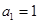 ,
,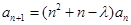 (
(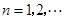 ),
),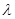 是常数.
是常数.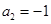 时,求
时,求 的值;
的值;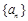 的前
的前 项和为
项和为 ,
, ,
, ,
,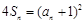 ,
, .
.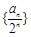 的前
的前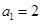 ,点
,点 在函数
在函数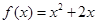 的图象上,其中
的图象上,其中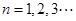
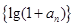 是等比数列,并求数列
是等比数列,并求数列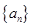 的通项公式;
的通项公式;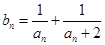 ,求数列
,求数列 的前
的前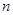 项和
项和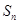 .
.
 行的第二个数为
行的第二个数为
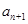 与
与 的递推关系(不必证明),并求出
的递推关系(不必证明),并求出 的通项公式
的通项公式 ,求证:
,求证: .
. 具有性质:①
具有性质:① 为整数;②对于任意的正整数
为整数;②对于任意的正整数 ,当
,当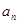 为偶数时,
为偶数时, ;当
;当 .
. 成等差数列,求
成等差数列,求 (
( 且
且 N),数列
N),数列 ,求证:
,求证: ;
; (
( N)时,都有
N)时,都有 .
.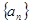 中,
中, 为常数,
为常数,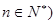 ,且
,且 成公比不等于1的等比数列.
成公比不等于1的等比数列. 的值;
的值; ,求数列
,求数列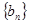 的前
的前 项和
项和 。
。