题目内容
已知数列 具有性质:①
具有性质:① 为整数;②对于任意的正整数
为整数;②对于任意的正整数 ,当
,当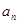 为偶数时,
为偶数时, ;当
;当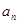 为奇数时,
为奇数时, .
.
(1)若 为偶数,且
为偶数,且 成等差数列,求
成等差数列,求 的值;
的值;
(2)设 (
( 且
且 N),数列
N),数列 的前
的前 项和为
项和为 ,求证:
,求证: ;
;
(3)若 为正整数,求证:当
为正整数,求证:当 (
( N)时,都有
N)时,都有 .
.
(1)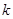 是奇数,则
是奇数,则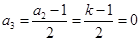 ,
, ,
,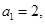 若
若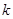 是偶数,则
是偶数,则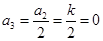 ,
, ,
,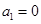
(2)根据数列的求和公式来证明不等式
(3)要证明对于当 (
( N)时,都有
N)时,都有 .,则要对于其通项公式分情况来得到其通项公式的表达式证明。
.,则要对于其通项公式分情况来得到其通项公式的表达式证明。
解析试题分析:⑴设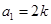 ,
,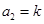 ,则:
,则: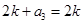 ,
,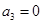
分两种情况: 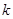 是奇数,则
是奇数,则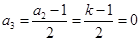 ,
, ,
,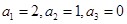
若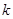 是偶数,则
是偶数,则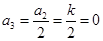 ,
, ,
,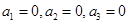
⑵当 时,
时,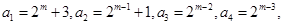

∴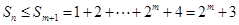
⑶∵ ,∴
,∴ ,∴
,∴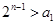
由定义可知: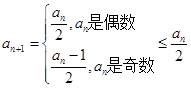 ∴
∴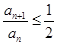
∴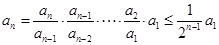
∴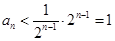
∵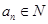 ,∴
,∴ ,
,
综上可知:当
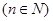 时,都有
时,都有
考点:数列的运用
点评:本试题主要是考查了等差数列和数列的求和,以及数列与不等式的证明,属于中档题。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 的前n项和为
的前n项和为 ,
, =1,且
=1,且
 .
. ,
, 的值,并求数列
的值,并求数列
 中,
中, ,前
,前 项的和为
项的和为 ,对任意的
,对任意的 ,
, ,
, ,
, 总成等差数列.
总成等差数列. 的值并猜想数列
的值并猜想数列 的通项公式
的通项公式
 .
.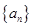 的前
的前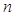 项和为
项和为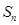 ,且
,且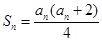
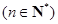 .
.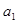 的值及数列
的值及数列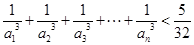
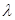 ,使不等式
,使不等式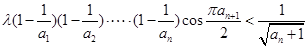
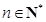 都成立?若存在,求出
都成立?若存在,求出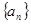 的前
的前 项和为
项和为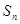
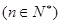 ,设
,设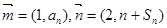 ,且
,且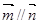 .
.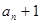 }是等比数列;
}是等比数列;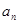 与
与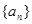 的首项为
的首项为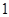 ,对任意的
,对任意的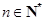 ,定义
,定义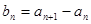 .
.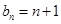 ,
, 的值和数列
的值和数列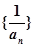 的前
的前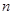 项和
项和 ;
;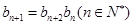 ,且
,且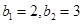 ,求数列
,求数列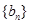 的前
的前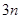 项的和.
项的和.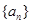 为公差不为
为公差不为 的等差数列,
的等差数列,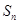 为前
为前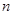 项和,
项和,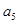 和
和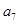 的等差中项为
的等差中项为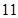 ,且
,且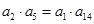 .令
.令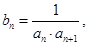 数列
数列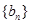 的前
的前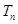 .
.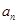 及
及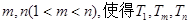 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的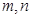 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意 ,总有
,总有 成等差数列.
成等差数列. ,求数列
,求数列 的前
的前 .
.