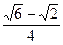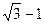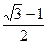题目内容
圆M与圆x2+y2=25内切,且经过点A(3,2),则圆心M在( )
| A.一个椭圆上 | B.双曲线的一支上 |
| C.一条抛物上 | D.一个圆上 |
圆x2+y2=25的圆心O(0,0),半径为:5.
设圆M的半径为r,∵圆M与圆x2+y2=25内切,且经过点A(3,2),
∴|MO|=5-r,并且|MA|=r,
∴|MO|+|MA|=5,又|OA|=
=
<5.
M满足椭圆的定义,∴M在椭圆上.
故选:A.
设圆M的半径为r,∵圆M与圆x2+y2=25内切,且经过点A(3,2),
∴|MO|=5-r,并且|MA|=r,
∴|MO|+|MA|=5,又|OA|=
| 32+22 |
| 13 |
M满足椭圆的定义,∴M在椭圆上.
故选:A.

练习册系列答案
相关题目
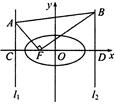
 ,与圆柱底面成
,与圆柱底面成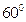 角的平面截这个圆柱得到一个椭圆,则这个椭圆的离心率为 。
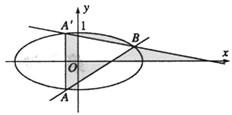
角的平面截这个圆柱得到一个椭圆,则这个椭圆的离心率为 。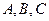 均在椭圆
均在椭圆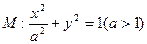 上,直线
上,直线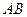 、
、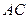 分别过椭圆的左右焦点
分别过椭圆的左右焦点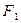 、
、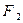 ,当
,当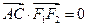 时,有
时,有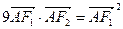 .
.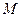 的方程;
的方程;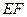 为圆
为圆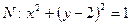 的任一条直径,求
的任一条直径,求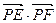 的最大值.
的最大值.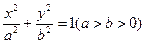 的左、右准线分别为
的左、右准线分别为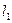 、
、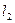 ,且分别交
,且分别交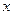 轴于
轴于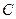 、
、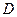 两点,从
两点,从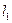 上一点
上一点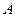 发出一条光线经过椭圆的左焦点
发出一条光线经过椭圆的左焦点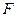 被
被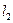 交于点
交于点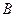 ,若
,若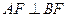 ,且
,且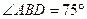 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )