题目内容
4、平面α外有两条直线m和n，如果m和n在平面α内的射影分别是m′和n′，给出下列四个命题：
①m′⊥n′?m⊥n；
②m⊥n?m′⊥n′；
③m′与n′相交?m与n相交或重合；
④m′与n′平行?m与n平行或重合．
其中不正确的命题个数是（ ）
①m′⊥n′?m⊥n；
②m⊥n?m′⊥n′；
③m′与n′相交?m与n相交或重合；
④m′与n′平行?m与n平行或重合．
其中不正确的命题个数是（ ）
分析：由射影的概念以及线线垂直关系的判定方法，观察具体的正方体判断，即可得答案．
解答：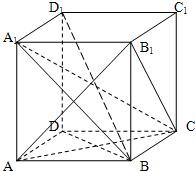
解：由射影的概念以及线线垂直关系的判定方法，观察如图的正方体：
∵AC⊥BD但A1C，BD1不垂直，故①错；
∵A1B⊥AB1但在底面上的射影都是AB故②错；
∵AC，BD相交，但A1C，BD异面，故③错；
∵AB∥CD但A1B，C1D异面，故④错
故选D
解：由射影的概念以及线线垂直关系的判定方法，观察如图的正方体：∵AC⊥BD但A1C，BD1不垂直，故①错；
∵A1B⊥AB1但在底面上的射影都是AB故②错；
∵AC，BD相交，但A1C，BD异面，故③错；
∵AB∥CD但A1B，C1D异面，故④错
故选D
点评：本题主要考查空间线面之间位置关系，以及射影的意义理解．关键是要理解同一条直线在不同平面上的射影不同；线在面内，线面平行，线面相交的不同位置下，射影也不相同．要从不用的方向看三垂线定理，充分发挥空间想象力．
练习册系列答案
相关题目