题目内容
平面α外有两条直线m和n,如果m和n在平面α内的射影分别是直线m1和直线n1,给出下列四个命题:
①m1⊥n1⇒m⊥n; ②m⊥n⇒m1⊥n1;③m1与n1相交⇒m与n相交或重合; ④m1与n1平行⇒m与n平行或重合;
其中不正确的命题个数是
①m1⊥n1⇒m⊥n; ②m⊥n⇒m1⊥n1;③m1与n1相交⇒m与n相交或重合; ④m1与n1平行⇒m与n平行或重合;
其中不正确的命题个数是
4
4
.分析:根据射影的概念,举例说明选项的错误,用证明的方法确定命题的正确性.
解答:解:①如图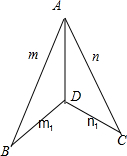 将正三角形ABC沿BC上的高AD折成直二面角,有m1⊥n1,但折后∠BAC 为锐角,m,n不垂直.故错误.
将正三角形ABC沿BC上的高AD折成直二面角,有m1⊥n1,但折后∠BAC 为锐角,m,n不垂直.故错误.
②如图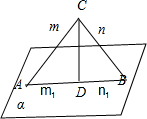 直角三角形ACB所在平面与α垂直,CD为斜边AB上的高线.有m⊥n,但m1与n1 不垂直,故错误.
直角三角形ACB所在平面与α垂直,CD为斜边AB上的高线.有m⊥n,但m1与n1 不垂直,故错误.
③如图 在正方体中,m1与n1相交,但m与n既不相交或也不重合,故错误.
在正方体中,m1与n1相交,但m与n既不相交或也不重合,故错误.
④如图,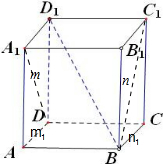 在正方体中,m1与n1平行,但m与n既不平行或也不重合,故错误
在正方体中,m1与n1平行,但m与n既不平行或也不重合,故错误
其中不正确的命题个数是4
故答案为:4
 将正三角形ABC沿BC上的高AD折成直二面角,有m1⊥n1,但折后∠BAC 为锐角,m,n不垂直.故错误.
将正三角形ABC沿BC上的高AD折成直二面角,有m1⊥n1,但折后∠BAC 为锐角,m,n不垂直.故错误. ②如图
 直角三角形ACB所在平面与α垂直,CD为斜边AB上的高线.有m⊥n,但m1与n1 不垂直,故错误.
直角三角形ACB所在平面与α垂直,CD为斜边AB上的高线.有m⊥n,但m1与n1 不垂直,故错误.③如图
 在正方体中,m1与n1相交,但m与n既不相交或也不重合,故错误.
在正方体中,m1与n1相交,但m与n既不相交或也不重合,故错误.④如图,
 在正方体中,m1与n1平行,但m与n既不平行或也不重合,故错误
在正方体中,m1与n1平行,但m与n既不平行或也不重合,故错误其中不正确的命题个数是4
故答案为:4
点评:本题考查射影的概念,直线和直线的位置关系.考查空间想象能力.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目