题目内容
平面a外有两条直线m和n,如果m和n在平面a内的射影分别是m1和n1,给出下列四个命题:①m1⊥n1⇒m⊥n
②m⊥n⇒m1⊥n1
③m1与n1相交⇒m与n相交或重合;
④m1与n1平行⇒m与n平行
其中不正确的命题个数是( )
A.1
B.2
C.3
D.4
【答案】分析:①可在正四棱锥中观察分析,从而否定①;
②可在满足m⊥n的三棱锥中,不满足m1⊥n1,从而否定②;
③m1与n1相交时,m与n可能异面,从而否定③;
④m1与n1平行,则m与n可能异面.
解答:解:对于①,在正四棱锥中,相邻的两条侧棱为m,n,其射影m1与n1为该正四棱锥的底面的两条对角线,但相邻的两条侧棱为m,n并不垂直,故①错误;
对于②,m⊥n时,m1与n1也可能重合,故②错误;
对于③,m1与n1相交时,m与n可能异面,m与n也可能相交或重合,故③错误;
对于④m1与n1平行,则m与n可能异面,也可能平行,故④错误.
故选D.
点评:本题考查命题的真假判断与应用,考查空间中直线与直线之间的位置关系,考查空间想象能力,属于中档题.
②可在满足m⊥n的三棱锥中,不满足m1⊥n1,从而否定②;
③m1与n1相交时,m与n可能异面,从而否定③;
④m1与n1平行,则m与n可能异面.
解答:解:对于①,在正四棱锥中,相邻的两条侧棱为m,n,其射影m1与n1为该正四棱锥的底面的两条对角线,但相邻的两条侧棱为m,n并不垂直,故①错误;
对于②,m⊥n时,m1与n1也可能重合,故②错误;
对于③,m1与n1相交时,m与n可能异面,m与n也可能相交或重合,故③错误;
对于④m1与n1平行,则m与n可能异面,也可能平行,故④错误.
故选D.
点评:本题考查命题的真假判断与应用,考查空间中直线与直线之间的位置关系,考查空间想象能力,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
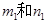 ,给出下列四个命题:
,给出下列四个命题: ; ②
; ②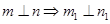
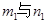 相交
相交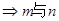 相交或重合 ④
相交或重合 ④