题目内容
(2012•宜宾一模)平面α外有两条直线m和n,如果m和n在平面α内的射影分别是m1和n1,给出下列四个命题:
①m1⊥n1⇒m⊥n;
②m⊥n⇒m1⊥n1
③m1与n1相交⇒m与n相交或重合
④m1与n1平行⇒m与n平行或重合
其中不正确的命题个数是( )
①m1⊥n1⇒m⊥n;
②m⊥n⇒m1⊥n1
③m1与n1相交⇒m与n相交或重合
④m1与n1平行⇒m与n平行或重合
其中不正确的命题个数是( )
分析:本题考查的知识点判断命题的真假,根据空间中特定的线线关系,分析它们在平面中射影的位置关系,或是由射影的位置关系,分析原直线的位置关系,根据直线的放置特点,逐一进行判断,可以得到正确结论.
解答:解:因为一个锐角在一个平面上的投影可以为直角,反之在平面内的射影垂直的两条直线所成的角可以是锐角,故①不正确.
两条垂直的直线在一个平面内的射影可以是两条平行直线,也可以是一条直线和一个点等其他情况,故②不正确.
两条异面直线在同一平面上的射影可以相交,所以射影相交的两条直线可以是异面直线,故③不正确.
两条异面直线在同一平面内的射影也可以平行,所以两直线的射影平行不一定有两直线平行或重合.故④不正确.
故选D.
两条垂直的直线在一个平面内的射影可以是两条平行直线,也可以是一条直线和一个点等其他情况,故②不正确.
两条异面直线在同一平面上的射影可以相交,所以射影相交的两条直线可以是异面直线,故③不正确.
两条异面直线在同一平面内的射影也可以平行,所以两直线的射影平行不一定有两直线平行或重合.故④不正确.
故选D.
点评:投影角度不同,空间中两直线在射影面上的位置关系就有变化,思考问题时应从多方面加以考虑.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
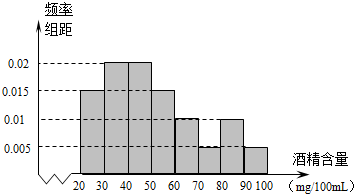 (2012•宜宾一模)《中华人民共和国道路交通安全法》
(2012•宜宾一模)《中华人民共和国道路交通安全法》